二叉堆

【二叉堆定义与存储结构】

二叉堆是具备以下性质的完全二叉树：

• 小根堆：每个结点的值都小于等于其左右孩子结点的值，堆顶元素是堆中最大值
• 大根堆：每个结点的值都大于等于其左右孩子结点的值，堆顶元素是堆中最小值

---

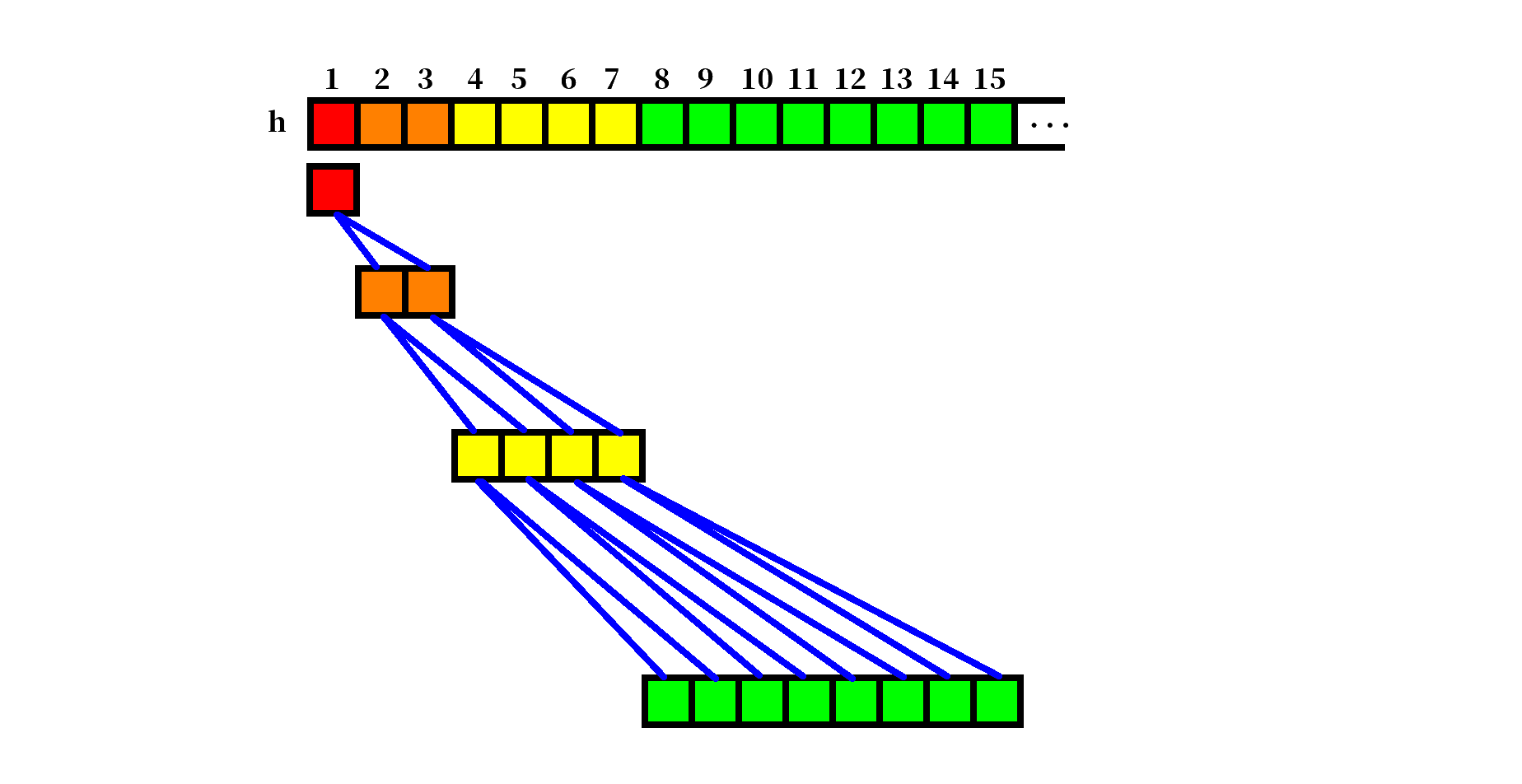
若将堆按照层序顺序从根结点开始编号，根结点序号为 $1$，用 $heap[i]$ 表示第 $i$ 个结点，则 $heap[i]$ 的两个儿子为：$heap[2i]$ 与 $heap[2i+1]$

且在小根堆中，满足：

$$\left\{\begin{matrix} heap[i] \leq heap[2i] \\ heap[i] \leq heap[2i+1] \end{matrix}\right.$$

在大根堆中，满足：

$$\left\{\begin{matrix} heap[i] \geq heap[2i] \\ heap[i] \geq heap[2i+1] \end{matrix}\right.$$

【插入操作与向上调整】

插入操作是指向二叉堆中插入一个元素，且要保证插入后二叉堆的结构不会改变

最简单的方式就是在最下一层最右边的叶结点后插入新的元素，若最后一层已满，就新增一层

以大根堆为例，在插入新结点后，如果这个结点的权值大于其父结点的权值，就进行向上调整操作，将其与其父结点进行交换，然后重复该过程，直到不满足或到根为止

同理，当堆为小根堆时，若这个结点的权值小于其父结点的权值，同样进行向上调整操作

向上调整操作的时间复杂度为 $O(\log n)$

大根堆的插入操作的实现如下：

int heap[N]; //heap[1]为堆顶
int size;   //堆指针
void up(int now) { //向上调整
    while (now > 1 && heap[now] > heap[now/2]) { //当前结点值小于其父结点值时终止
        int next = now >> 1;         //当前结点的父结点
            break;
        swap(heap[now], heap[now/2]); //交换元素
        now /= 2; //令now指向其父结点
    }
}
void insert(int x) { //插入操作
    heap[++size] = x; //在堆尾加入元素
    up(size); //从新加入的结点size开始向上调整
}

【删除操作与向下调整】

插入操作是指删除二叉堆的堆顶元素，且要保证删除后二叉堆的结构不会改变

如果直接进行删除，那么堆会变为两个，难以处理

因此，可以将删除操作等价为插入操作的逆过程，即设法将根结点移动到二叉堆中的最后一个结点，然后再进行删除

通常的做法是，先将根结点与最后一个结点交换，然后删除位于最后一个结点处的根结点

但这样新得到的堆显然不满足堆的性质，为此，要进行向下调整

同样以大根堆为例，在得到新的堆后，在新堆的根结点的儿子中，找一个值最大的结点，然后将他们交换，并重复该过程，直到底层为止

同理，当堆为小根堆时，找一个值最小的儿子结点，进行向下调整操作即可

向下调整操作的时间复杂度为 $O(\log n)$

int heap[N]; //heap[1]为堆顶
int size;    //堆指针
int down(int now) {
    while (now * 2 <= size && heap[now*2] > heap[now]) { //当前结点值小于其子结点值时终止
        int next = now *2; //当前结点的子结点
        if (next < size && heap[next + 1] < heap[next]) //比较左右孩子，指向较大者
            next++;
        swap(heap[now], heap[next]); //交换元素
        now = next;
    }
}
int del(int x) { //删除操作
    int res = heap[1]; //要删除的结点
    heap[1] = heap[size--]; //尾结点提升到根结点    
    down(1); //从根结点1开始向下调整
    return res;
}

【堆的建立】

对于一个空的二叉堆，当从头开始建立时，若不考虑元素顺序，只需要一个个的将 $n$ 个元素进行插入操作，之后，从根开始，按 BFS 序进行向上调整，使得建立的二叉堆满足堆的性质

int heap[N]; //heap[1]为堆顶
int size;   //堆指针
void up(int now);   //向上调整
void buildHeap(int a[], int n) {
    for (int i = 1; i <= n; i++) //不考虑元素顺序插入n个元素
        heap[++size] = a[i];
    for (int i = 1; i <= n; i++) //从根结点开始向上调整
        up(i);
}

这样一来，对于第 $k$ 层的结点，向上调整的复杂度为 $O(k)$，而不是 $O(\log n)$

但以总时间复杂度来说，有：

$$\log 1+\log 2 +...+\log n=O(n\log n)$$

为此，可以换一种思路，即在对 $n$ 个元素插入后，从叶结点开始进行向下调整

int heap[N]; //heap[1]为堆顶
int size;   //堆指针
void down(int now);   //向下调整
void buildHeap(int a[], int n) {
    for (int i = 1; i <= n; i++) //不考虑元素顺序插入n个元素
        heap[++size] = a[i];
    for (int i = n; i >= 1; i--) //从叶结点开始向下调整
        down(i);
}

可以发现，叶结点无需调整，且结点向下调整的时间复杂度为 $O(\log n-k)$

因此，可以从序列约 $\frac{n}{2}$ 的位置处开始调整，从而在不影响复杂度的情况下减少参数，以总时间复杂度来说，有：

$$\begin{align} & n\log n-\log 1-\log 2-...-\log n \notag \\ \leq & n\log n-0\times 2^0-1\times2^1-...-(\log n-1)\times\frac{n}{2} \notag \\ =& n\log n -(n-1)-(n-2)-(n-4)-...-(n-\frac{n}{2}) \notag \\ =& n\log n- n\log n+1+2+4+...+\frac{n}{2} \notag \\ =& n-1 \notag \\ =& O(n) \notag \end{align}$$

之所以能够以 $O(n)$ 的方式建堆，是因为堆的形式很弱，二叉堆并不是唯一的