并查集的删除操作

在并查集中，删除操作是指删除掉并查集中的一个结点

在所有结点都直接连接在根结点上的完美并查集上，理论上只要把要删除的节点的上级重新指向自己就可以了

但实际情况中，并查集形成的树的形态都是不可预估的，如果一个结点非叶结点，将该结点直接删除，会将其与其子孙结点一起删除

所以在一个需要删除的并查集中，可以进行如下处理：

将每一个结点都设立一个虚拟父结点，这样根结点就是我们设立的虚拟结点，类似于将每个结点放到一个盒子中
如果删除某结点，那么可以修改当前结点的父结点来导致当前结点的孤立，即删除时把这个结点从当前盒子拿出来，放到另一个盒子中

由于结点之间都是通过盒子来确定关系的，所以盒子中的元素是否存在并不影响结点之间的关系，以下图为例：

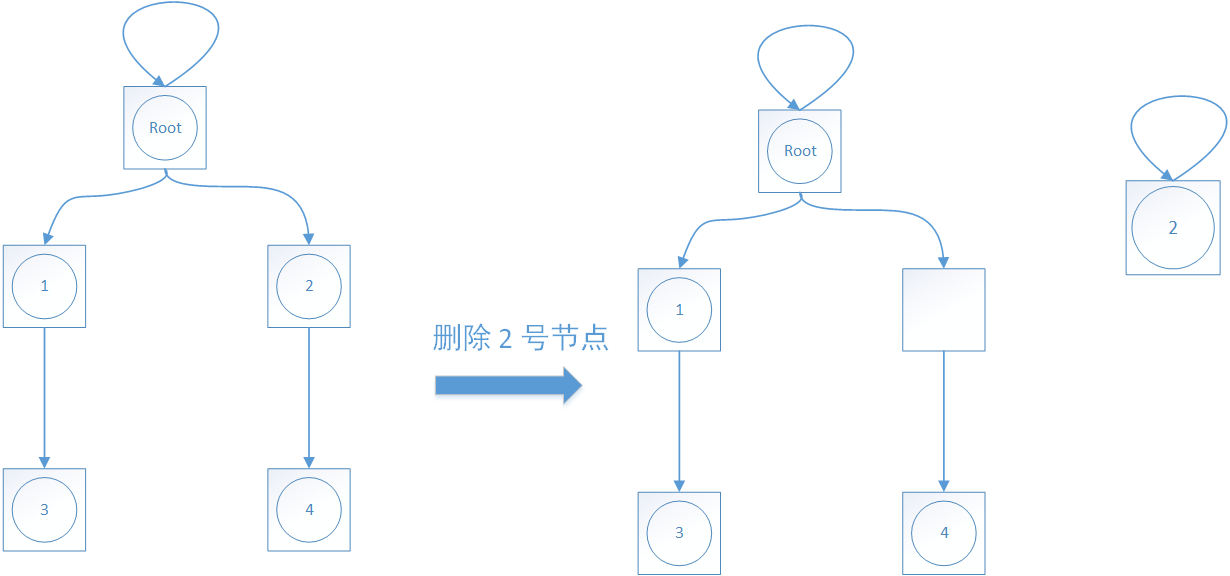
如果要删除 $2$ 号结点，那么将把 $2$ 号结点拿出来放到另一个盒子中就可以了，可以看到原来的那个树结构并没有发生变化，但是 $2$ 号结点已经不在这里面了

实现：

//假设最多会有n个结点，就从n+1开始作为假结点
int index;  //存放盒子结点使用到哪一个
int pre[N]; //盒子结点
void init (int n) { //初始化
    index = n;
    for(int i = 0; i < n; i++) //普通节点指向他的盒子节点
        pre[i] = index++;
    for(int i = n; i < 2*n; i++)//盒子节点指向自己就像一般的并查集一样
        pre[i] = i;
}
void del (int n) {  //删除结点
    pre[n] = index; //将要删除的节点重新指向一个新的盒子
    pre[index] = index++; //盒子节点指向自己
}