【基本思想】

原始冒泡排序是交换排序中最简单的排序方法，其基本思想是：两两比较相邻记录的关键码，若反序则交换，直到没有反序为止

原始冒泡排序的具体的排序过程如下：

1）将整个待排序的序列分为有序区和无序区，初始时有序区为空，无序区包含所有待排序记录

2）对无序区从前向后依次将相邻记录关键码进行比较，若反序则交换，从而使得关键码小的记录前移，关键码大的记录后移

3）重复执行步骤 2，直到无序区没有反序记录

需要注意的是，冒泡排序中产生的有序子序列一定是全局有序的，即有序子序列中的所有元素的关键字一定是小于或大于子序列中所有元素的关键字，每趟排序都会将一个元素放到其最终的位置上

原始冒泡排序的宏观排序过程如下图

【实例】

以数列 $\{6,5,3,1,8,7,2,4\}$ 为例，演示原始冒泡排序过程：

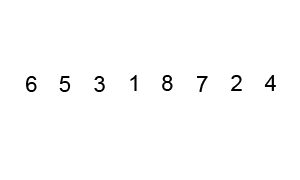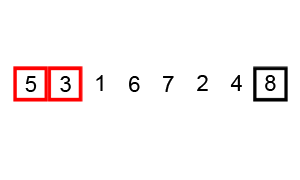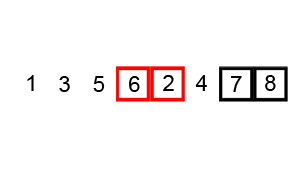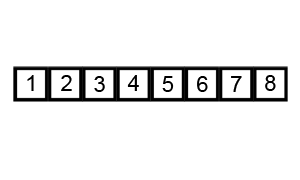
由此，可列出每一趟的结果，可以发现，在第 $6$ 趟时，未发生交换，此时数列已经有序

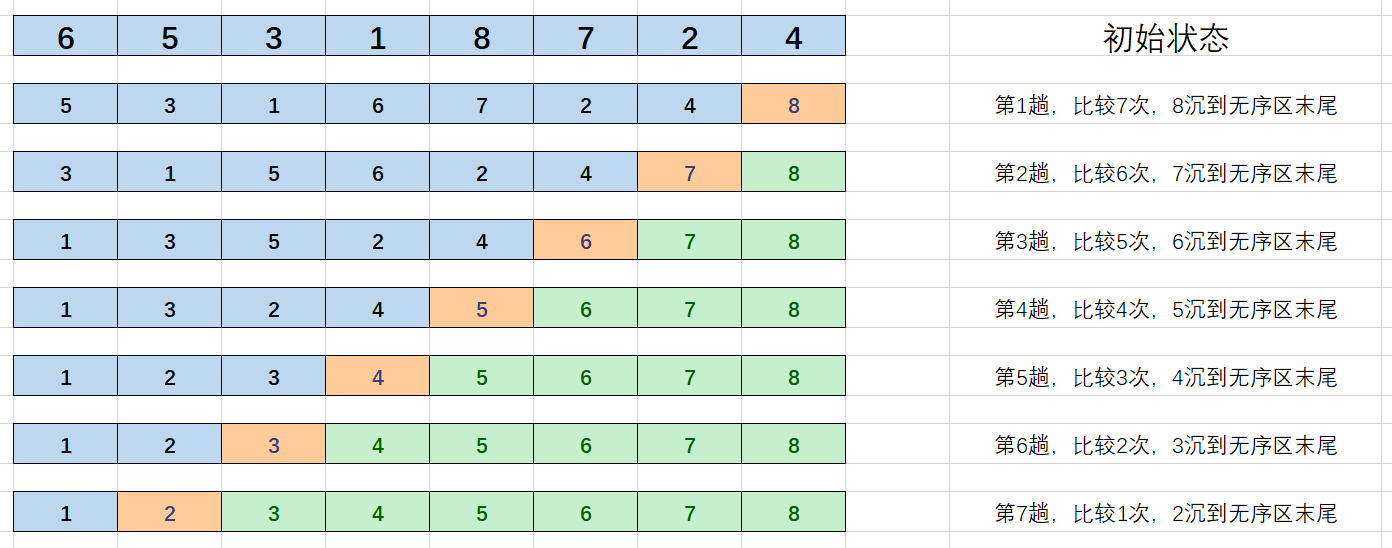
因此，在冒泡排序中，当某一趟比较时未发生交换，说明表已经有序

【性能分析】

冒泡排序适用于顺序存储、链式存储结构，由于当 $i>j$，且 $a[i]=a[j]$ 时，不会发生交换，因此其是一种稳定排序算法

冒泡排序仅需常数个辅助空间，作为待插入记录的暂存单元，因此空间复杂度为：

$O(1)$

在最好情况下，待排序序列为正序，要进行 $n-1$ 趟排序，每趟仅比较 $1$ 次，共比较 $n-1$ 次，移动 $0$ 次，因此，最优时间复杂度为：

$O(n)$

在最坏情况下，待排序序列为逆序，要进行 $n-1$ 趟排序，第 $i$ 趟比较 $n-i$ 次，每次移动 $3$ 次来进行交换，那么总比较次数为 $\frac{n(n+1)}{2}$，总移动次数为 $\frac{3n(n-1)}{2}$，因此，最坏时间复杂度为：

$O(n^2)$

在平均情况下，待排序序列中各种可能排列的概率情况相同，在插入第 $i$ 个记录时平均要比较有序区中全部记录的一半，那么总的比较次数与移动次数均约为 $\frac{n^2}{4}$，因此，平均时间复杂度为：

$O(n^2)$

【实现】

朴素实现

void bubbleSort (int a[], int n) {
    for (int i = 1; i <= n - 1; i++) //比较n-1趟
        for (int j = 1; j <= n - i; j++) //每趟交换n-i次
            if(a[j] > a[j+1])
                swap(a[j], a[j+1]);
}

判断优化

void bubbleSort (int a[], int n) {
    for (int i = 1; i <= n - 1; i++) { //比较n-1趟
        bool flag = false; //判断是否有交换
        for (int j = 1; j <= n - i; j++) { //每趟交换n-i次
            if (a[j] > a[j+1]) {
                swap(a[j], a[j+1]);
                flag = true; //有交换说明仍需排序
            }
        }
        if (!flag) //若本趟无交换，说明表已经有序，终止
            break;
    }
}