【引入】
在进行外部排序时,当其进行内部归并时,要在 $k$ 个元素中选择关键字最小的记录需要比较 $k-1$ 次,每趟归并 $n$ 个元素需要做 $(n-1)(k-1)$ 次比较,$S$ 趟归并总共需要比较的次数为:
在 外部排序 中讨论过,增大归并路数 $k$ 或减少初始归并段个数 $r$,都可以减少归并趟数 $S$,进而减少 I/O 次数,以提高外部排序速度
对于增加归并路数 $k$ 来说,$\frac{k-1}{\left \lceil log_2k \rceil \right.}$ 随着 $k$ 增长而增长,因此内部归并时间随着 $k$ 的增长而增长,这抵消了由于增大 $k$ 而减少外存访问次数所得到的效益,故而不能使用普通的内部归并排序算法
为使内部归并不受 $k$ 增大的影响,引入了败者树
【败者树】
败者树是树形选择排序的一种变体,可视为一棵完全二叉树
$k$ 个叶结点分别存放 $k$ 个归并段在归并过程中当前参加比较的记录,内部结点用于记录左右子树中的失败者,而让胜者继续向上进行比较,直到根结点
对于比较的两个数,大者为失败者,小者为胜利者,根结点指向的数为最小数
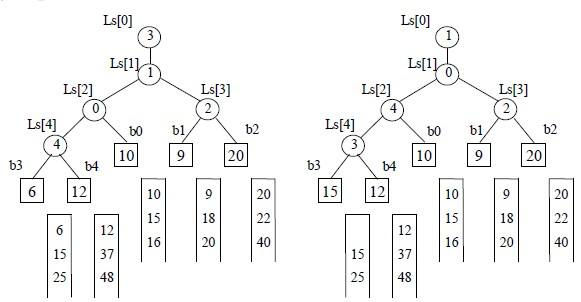
如下图所示,初始时,叶结点 $b_3$ 与 $b_4$ 比较,$b_4$ 是败者,段号 $4$ 写入父结点 $ls[4]$,叶结点 $b_1$ 与 $b_2$ 比较,$b_2$ 是败者,段号 $2$ 写入父结点 $ls[3]$
之后,$b_3$ 与 $b_4$ 的胜者 $b_3$ 与叶结点 $b_0$ 比较,$b_0$ 是败者,段号 $0$ 写入父结点 $ls[2]$
最后两个胜者 $b_3$ 与 $b_1$ 比较,$b_1$ 是败者,段号 $1$ 写入父结点 $ls[1]$,$b_3$ 是胜者,段号 $3$ 写入根结点 $ls[0]$
此时,根结点 $ls[0]$ 所指的段的关键字最小,将 $b_3$ 中的 $6$ 输出后,将下一关键字 $15$ 填入 $b_3$,继续进行上述过程
【性能分析】
$k$ 路归并的败者树深度为 $\left \lceil log_2k \rceil \right.$,因此 $k$ 个记录中选择最小关键字,最多需要 $\left \lceil log_2k \rceil \right.$ 次比较,因此总的比较次数为:
可见,使用败者树后,内部归并的比较次数与 $k$ 无关,因此,只要内存空间允许,增大归并路数 $k$ 将有效地减少归并树的高度,从而减少 I/O 次数,提高外部排序的速度
值得说明的是,归并路数 $k$ 并非越大越好,归并路数 $k$ 增大时,相应地需要增加输入缓冲区的个数,若可供使用的内存空间不变,势必要减少输入缓冲区的容量,使得内存、外存交换数据的次数增大,当 $k$ 值过大时,虽然归并趟数会减少,但读写外存的次数仍会增大

