【基本思想】

直接插入排序是最简单、最直观的插入类排序算法，其是一种稳定的排序方法，类似于玩扑克时整理手牌的过程

其排序过程为：

1）将整个待排序的记录序列划分为有序区和无序区

2）初始时，有序区为待排序记录序列中的第一个记录，无序区包括所有剩余待排序的记录

3）每次将无序区的第一个记录插入到有序区的合适位置中，从而使无序区减少一个记录，有序区增加一个记录

4）重复执行步骤 3），直到无序区中没有记录

直接插入排序的宏观过程如下图所示

【实例】

以数列 $\{12,15,9,20,6,31,24\}$ 为例，给出直接插入排序的每一趟的排序结果：

以数列 $\{6,5,3,1,8,7,2,4\}$ 为例，给出直接插入排序的排序过程：

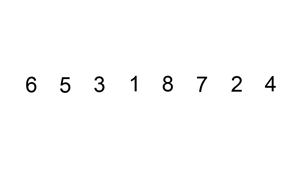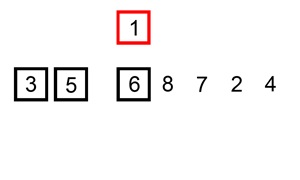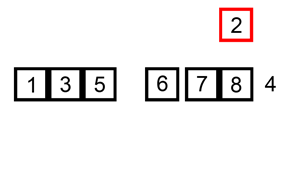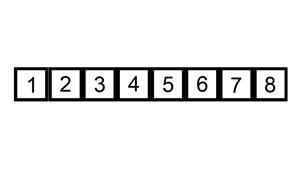
【性能分析】

直接排序适用于顺序存储、链式存储方式，每次插入的元素总是从前向后先比较再移动，不会出现两个相同元素相对位置发生变化的情况，是一稳定排序算法

在排序过程中，仅需一个辅助空间，作为待插入记录的暂存单元和插入过程中的哨兵，因此空间复杂度为 $O(1)$

在最好情况下，待排序序列为正序，每趟排序只需与最后一个记录比较一次，移动两次记录，那么总比较次数为 $n-1$，总移动次数为 $2(n-1)$，因此，最优时间复杂度为

$O(n)$

在最坏情况下，待排序序列为逆序，第 $i$ 趟插入时，第 $i$ 个记录必须与前面的 $i-1$ 个记录的关键码与哨兵比较，并且每比较一次就要做一次记录的移动，那么总比较次数为 $\frac{n(n+1)}{2}$，总移动次数为 $\sum\limits_{i=2}^n(i+1)$，因此，最坏时间复杂度为

$O(n^2)$

在平均情况下，待排序序列中各种可能排列的概率情况相同，在插入第 $i$ 个记录时平均要比较有序区中全部记录的一半，那么总的比较次数与移动次数均约为 $\frac{n^2}{4}$，因此，平均时间复杂度为

$O(n^2)$

【实现】

void insertSort (int a[], int n) {
    for (int i = 2; i <= n; i++) { //n-1趟比较，a[2]~a[n]依次插入
        if (a[i] < a[i-1]) {
            int temp = a[i]; //设置哨兵
            for (int j = i - 1; temp < a[j]; j--) //寻找插入位置
                a[j+1] = a[j]; //记录后移
            a[j+1] = temp; //复制到插入位置
        }
    }
}