【基本思想】

对于直接插入排序，当待排序列为正序时，其时间复杂度可提高到 $O(n)$，故而其更适用于基本有序或数据量不大的排序表，针对这两点，对直接插入排序进行改进，即希尔排序

所谓基本有序，就是小的关键字基本在前，大的关键字基本在后，但基本有序的条件十分苛刻，难以达到，为了达到基本有序，采用跳跃分割策略，即将相距某个增量的记录组成一个子序列，这样保证子序列内分别进行直接插入排序得到的结果是基本有序而非局部有序

希尔排序的基本思想是：将整个待排序记录序列分割成若干个子序列，在子序列内分别进行直接插入排序，待整个序列基本有序时，再对全体记录进行一次直接插入排序

简单来说，希尔排序就是在直接插入排序的基础上，将直接插入排序中的 $1$ 全部改为增量 $d$

【算法步骤】

希尔排序的算法步骤如下：

1）从第一个元素开始，选择一个增量序列 $\{d_1,d_2,..,d_k\}$，该序列从 $d_1<n$ 开始，严格递减，直到 $d_k=1$

2）按增量序列个数 $k$，对序列进行 $k$ 趟直接插入排序

3）每趟排序，根据对应的增量 $d_i$，将待排序列分割成若干长度为 $m$ 的子序列，分别对各子表进行直接插入排序，仅增量因子为 $1$ 时，整个序列作为一个表来处理，表长度即为整个序列的长度

目前为止，尚未有一个最好的增量序列，一般取：

$d_1= \left \lfloor \frac{n}{2} \right \rfloor, d_{i+1}=\left \lfloor \frac{d_i}{2} \right \rfloor$

直到最后一个增量 $d_k=1$

希尔排序的宏观过程如下图所示

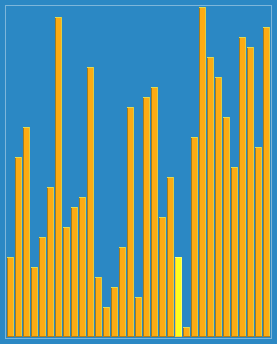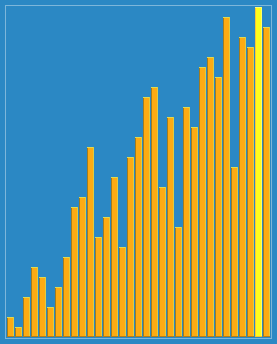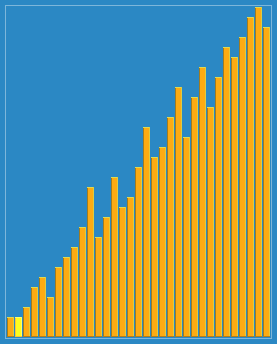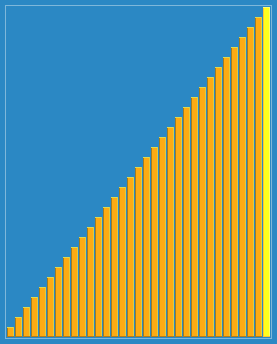
【实例】

下面以数列 $\{80,30,60,40,20,10,50,70\}$ 为例，演示希尔排序过程

数列中有 $8$ 个元素，即 $n=8$，那么有：

第一趟：取 $d_1=4$，分为 $4$ 组

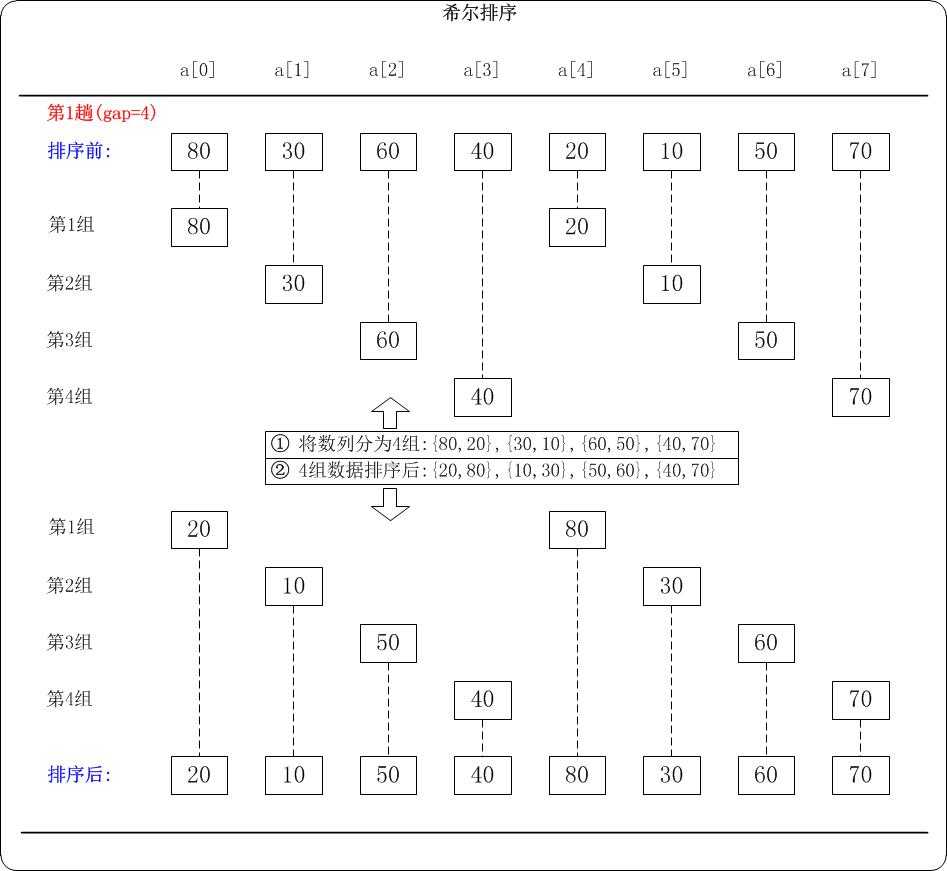
第二趟：取 $d_2=2$，分为 $2$ 组

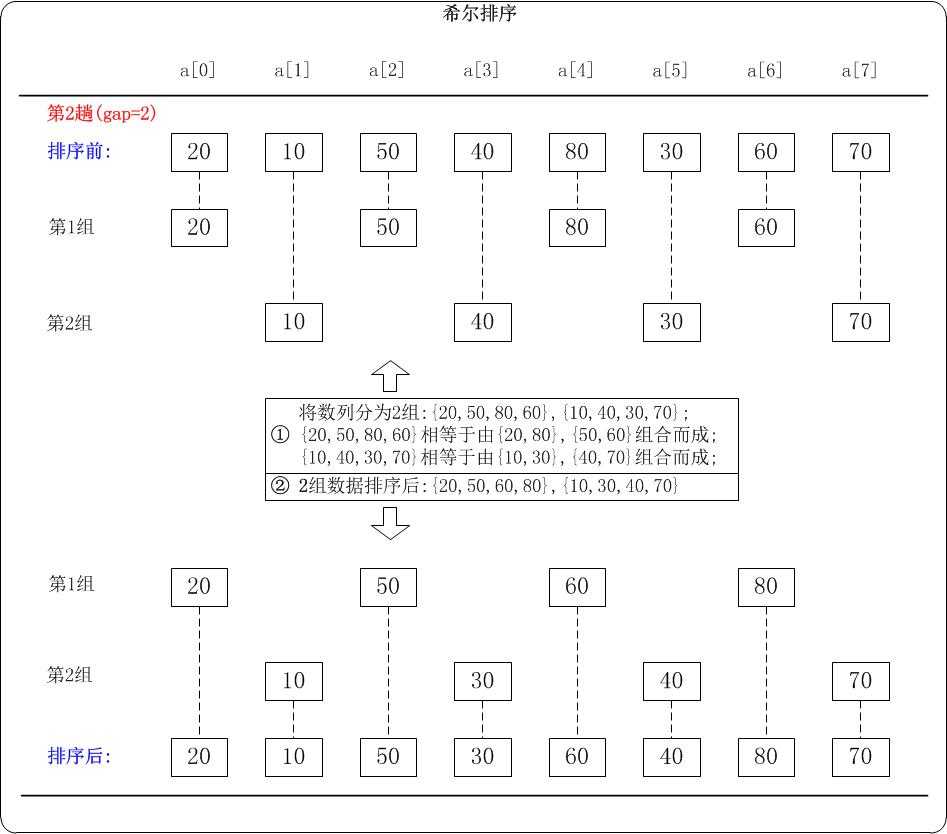
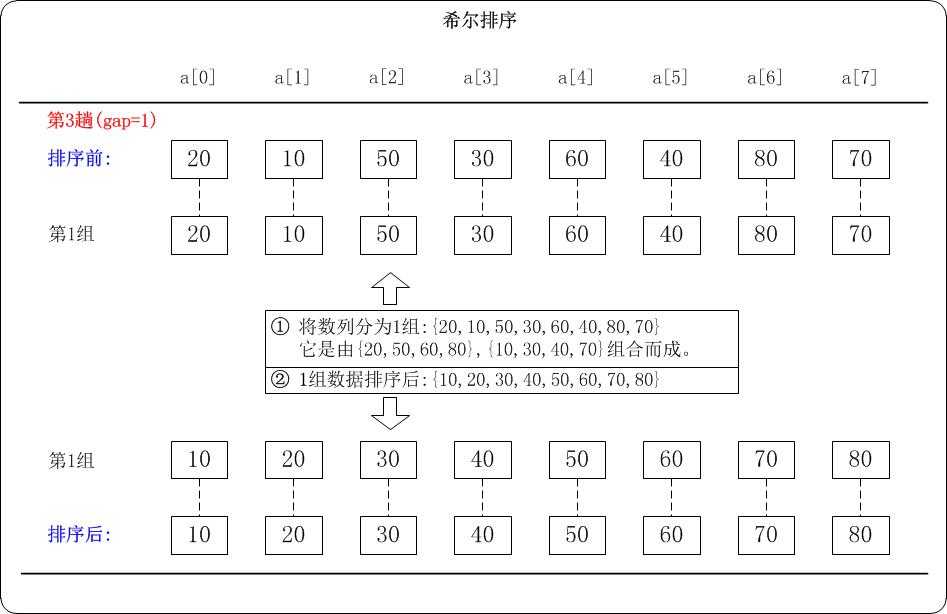
第三趟：取 $d_3=1$，分为 $1$ 组，排序完成

【性能分析】

希尔排序适用于顺序存储方式，由于当相同关键字记录被划分到不同子表时，可能会改变相对次序，因此希尔排序是不稳定排序算法

在希尔排序过程中，需要常数个辅助空间，作为待插入记录的暂存单元，因此其空间复杂度为

$O(1)$

希尔排序的时间复杂度依赖于增量序列的函数，这涉及到数学上尚未解决的难题

但当 $n$ 在某特定范围时，其时间复杂度约为 $O(n^{1.3})$，最坏情况下为 $O(n^2)$

【实现】

void shellSort (int a[], int n) {
    for (int d = n/2; d >= 1; d = d/2) { //增量
        for (int i = d + 1; i <= n; i++) { //对每一组直接插入排序
            if (a[i] < a[i-d]) {
                int temp = a[i]; //暂存a[i]
                for (int j = i - d; i > 0 && temp < a[j]; j = j - d) //记录后移
                    a[j+d] = a[j];
                a[j] = temp;  //复制到插入位置
            }
        }
    }
}