【进程同步与进程互斥的实现】
进程同步
假设有两个并发执行的进程 $P_1$ 与 $P_2$,$P_1$ 中有语句 $S_1$,$P_2$ 中有语句 $S_2$,现们希望 $S_1$ 执行后再执行 $S_2$
为实现这样的同步关系,可令进程 $P_1$、$P_2$ 共享一个初值为 $0$ 的公用信号量 $S$,将 signal(S) 放在 $S_1$ 语句后面,将 wait(S) 放在 $S_2$ 语句前面
这样一来,若 $P_2$ 先执行 wait(S) 时,会将进程阻塞,并放入阻塞队列中,当进程 $P_1$ 中的 $S_1$ 执行完后,执行 signal(S) 操作,将 $P_2$ 从阻塞队列中放回就绪队列,当 $P_2$ 得到处理机时,即可继续执行,从而使得当语句 $S_1$ 执行完后,语句 $S_2$ 才可以执行
1
2
3
4
5
6
7
8
9
| Semaphore S = 0;
void process1() {
S1;
signal(S);
}
void process2() {
wait(S);
S2;
}
|
进程互斥
当多个进程需要互斥地访问某临界资源时,仅需为该资源设置一初值为 $1$ 的互斥信号量 mutex,然后将各进程访问该资源的临界区置于 wait(mutex) 与 signal(mutex) 之间即可
1
2
3
4
5
6
7
8
9
10
11
12
13
| Semaphore mutex = 1;
void P1() {
wait(mutex);
critical section;
signal(mutex);
remainder section;
}
void P2() {
wait(mutex);
critical section;
signal(mutex);
remainder section;
}
|
当没有进程在临界区时,任意一个进程在进入临界区前会执行 $P$ 原语,将资源量 $S$ 减为 $0$,然后进入临界区;当有进程存在于临界区时,$S=0$,再有进程要进入临界区时,执行 $P$ 操作将会阻塞,直到在临界区中的进程退出
【前驱关系问题】
当多个进程之间或语句之间存在前驱关系时,会根据前驱图分析每一对前驱关系,为每一对前驱关系设置一个同步信号量,以保证进程或语句的顺序执行
关于前驱图,详见:前驱图与进程图
假设存在 $P_1$、$P_2$、$P_3$、$P_4$、$P_5$、$P_6$ 这 $6$ 个进程,每个进程中只有 $S_i$ 这一条语句,这 $6$ 个进程的前驱图如下所示
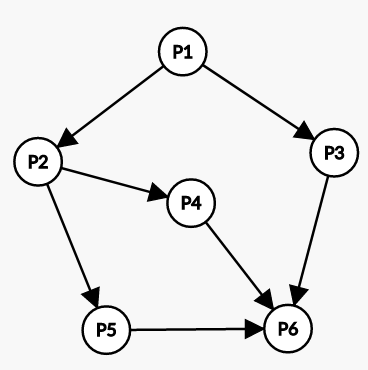
可以发现,前驱图中存在 $P_1\rightarrow P_2$、$P_1\rightarrow P_3$、$P_2\rightarrow P_4$、$P_2\rightarrow P_5$、$P_3\rightarrow P_6$、$P_4\rightarrow P_6$、$P_5\rightarrow P_6$ 这 $7$ 个前驱关系,为使得各程序段间能正常执行,设置 $7$ 个同步信号量,分别代表上述的 $7$ 个前驱关系,之后对每个前驱关系与同步信号量,采用进程同步的方法即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
| semaphore p12 = 0;
semaphore p13 = 0;
semaphore p24 = 0;
semaphore p25 = 0;
semaphore p36 = 0;
semaphore p46 = 0;
semaphore p56 = 0;
void P1() {
S1;
signal(p12);
signal(p13);
}
void P2() {
wait(p12);
S2;
signal(p24);
signal(p25);
}
void P3() {
wait(p13);
S3;
signal(p36);
}
void P4() {
wait(p24);
S4;
signal(p46);
}
void P5() {
wait(p25);
S5;
signal(p56);
}
void P6() {
wait(p36);
wait(p46);
wait(p56);
S3;
}
|
【生产者-消费者问题】
1.问题描述
一组生产者进程和一组消费者进程共享一个初值为空,大小为 $n$ 的缓冲区,只有缓冲区未满时,生产者才能将产品放入缓冲区中,否则必须等待;只有缓冲区不空时,消费者才能从缓冲区中提取出产品,否则必须等待,同时,缓冲区是临界资源,任一时刻只允许一个生产者放入产品或一个消费者提取产品
2.问题分析
可以发现,生产者和消费者对缓冲区的访问是互斥关系,同时生产者和消费者又存在同步关系,只有生产者生产后,消费者才能消费
为此,设置一个初值为 $1$ 的互斥信号量 mutex,用来互斥访问缓冲区,再设置一个初值为 $0$ 的记录当前缓冲区中存放产品格子的数量的信号量 full,还需设置一个初值为 $n$ 的记录当前缓冲区中未存放产品格子的数量的信号量 empty,用来标志缓冲区已空
3.实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| semaphore mutex = 1;
semaphore empty = n;
semaphore full = 0;
void producer() {
while (true) {
生产产品;
P(empty);
P(mutex);
放入缓冲区;
V(mutex);
V(full);
}
}
void consumer() {
while (true) {
P(full);
P(mutex);
放入缓冲区;
V(mutex);
V(empty);
使用产品;
}
}
|
【多生产者消费者问题】
1.问题描述
桌上有一个盘子,每次只能放一个水果,父亲只能向盘子里放苹果,母亲只能向盘子里放橘子,女儿专门吃苹果,儿子专门吃橘子,只有盘子中有水果时,女儿或儿子才能吃水果,同时,盘子是临界资源,任一时刻只允许父亲或母亲放入水果,儿子或女儿吃水果
2.问题分析
可以发现,该问题是生产者与消费者问题的改进,即存在两个生产者、两个消费者,缓冲区大小为 $1$
对盘子的访问是互斥关系,同时父亲和女儿、母亲和儿子间存在两对同步关系,即父亲放完苹果后女儿要立刻吃,母亲放完橘子后儿子要立刻吃
为此,设置一个初值为 $1$ 的互斥信号量 mutex,用来互斥访问盘子,再设置一个初值为 $0$ 的表示父女间前驱关系的同步信号量 apple,一个初值为 $0$ 的表示母子间前驱关系的同步信号量 orange
3.实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| semaphore mutex = 1;
semaphore apple = 0;
semaphore orange = 0;
void father() {
while (true) {
准备苹果;
P(mutex);
向盘子中放苹果;
V(apple);
}
}
void daughter() {
while (true) {
P(apple);
从盘子中拿苹果;
V(mutex);
吃苹果;
}
}
void mother() {
while (true) {
准备橘子;
P(mutex);
向盘子中放橘子;
V(orange);
}
}
void son() {
while (true) {
P(orange);
从盘子中拿橘子;
V(mutex);
吃苹果;
}
}
|
【吸烟者问题】
1.问题描述
有三个抽烟者,一个供应者,抽烟者不停的卷烟并抽烟,其需要三种材料:烟草、纸、胶水,三个人中,第一个有胶水,第二个有纸,第三个有烟草;供应者无限提供这三种材料,每次随机将两种不同的材料放到桌上,拥有剩下那种材料的抽烟者就会拿起桌上的材料卷烟并抽掉,同时告诉供应者已完成,供应者又会随机再提供两种材料,如此往复
2.问题分析
可以发现,总共存在 $4$ 个进程,一个进程负责提供材料,剩下三个负责卷烟抽烟
供应者和每个抽烟者之间都存在一对同步关系,只有供应者提供材料后,抽烟者才可以卷烟抽烟,同时,供应者无法同时满足两个及以上的抽烟者,彼此之间存在互斥关系,此外,在一个抽烟者完成后,会通知供应者,这里也存在一个同步关系
为此,设置三个初值为 $0$ 的同步量 offer1、offer2、offer3,分别表示供应者提供的烟草与纸、烟草与胶水、纸与胶水,设置一个初值为 $0$ 的同步量 finish,来代表抽烟者通知供应者提供材料
由于每次供应者提供材料是随机提供两种的,为此要设置一个随机数再模 $3$,根据结果令供应者每次随机提供两种材料
3.实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| int random;
semaphore offer1 = 0;
semaphore offer2 = 0;
semaphore offer3 = 0;
semaphore finish = 0;
void supply() {
while (true) {
seed = time(0);
srand(seed);
random = rand();
random %= 3;
if (random == 0)
V(offer1);
else if (random == 1)
V(offer2);
else
V(offer3);
将材料放到桌子上;
P(finish);
}
}
void smoke1() {
while (true) {
P(offer1);
拿材料、卷烟、抽烟;
V(finish);
}
}
void smoke2() {
while (true) {
P(offer2);
拿材料、卷烟、抽烟;
V(finish);
}
}
void smoke3() {
while (true) {
P(offer3);
拿材料、卷烟、抽烟;
V(finish);
}
}
|
【读写者问题】
1.问题描述
存在读、写两组并发进程,共享一个文件,允许当两个及以上读进程时,但当某个写进程与其他进程同时访问时,会出现错误,为此要求:
- 允许多个读进程同时读
- 任一时刻只允许一个写进程写
- 任一写进程写完前不允许其他进程工作
- 写进程写前应让已有进程退出
2.问题分析
可以发现,读进程与写进程间存在互斥关系,写进程与其他任意进程存在互斥关系,此外,还应记录有几个读者在读
为此,设置一个初值为 $0$ 的计数器 count 来记录读者数量,还要设置一个互斥信号量 mutex 来防止更新 count 时出现错误,一个互斥信号量 rw 来用于读写进程互斥访问文件
3.实现
由于未说明读、写进程间是否存在优先级,为此分别给出读进程优先、写进程优先的实现
读进程优先:可能会导致写进程饿死
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| int count = 0;
semaphore mutex = 1;
semaphore rw = 1;
void writer() {
while (true) {
P(rw);
向文件中写入;
V(rw);
}
}
void read() {
while (true) {
P(mutex);
if (count == 0)
P(rw);
count++;
V(mutex);
从文件中读取;
P(mutex);
count--;
if (count == 0)
V(rw);
V(mutex);
}
}
|
写进程优先:读写公平,优先级相同
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| int count = 0;
semaphore mutex = 1;
semaphore rw = 1;
semaphore w = 1;
void writer() {
while (true) {
P(w);
P(rw);
向文件中写入;
V(rw);
V(w);
}
}
void read() {
while (true) {
P(w);
P(mutex);
if (count == 0)
P(rw);
count++;
V(mutex);
V(w);
从文件中读取;
P(mutex);
count--;
if (count == 0)
V(rw);
V(mutex);
}
}
|
【哲学家进餐问题】
1.问题描述
一个圆桌上有 $n$ 个哲学家,每两人之间摆一根筷子,中间一碗米饭,哲学家只进餐、思考,思考时不影响他人,进餐时试图拿起左右两根筷子,若筷子已经在他人手上,则进行等待,当进餐完毕后,放下筷子,进行思考
2.问题分析
对于 $n$ 个哲学家来说,其与左右相邻的人对其中间的筷子进行互斥访问
为此,对于 $n$ 根筷子来说,每根筷子设置一个互斥信号量,从而构成一个互斥信号量组 chopsticks[n],再令哲学家编号从 $0$ 到 $n-1$,规定 $i$ 号左边筷子为 $i$,右边筷子为 $(i+1)\%n$
而对于 $n$ 个哲学家进程来说,最简单的方法是同时拿起左右两根筷子,但这可能造成死锁,为避免死锁,有以下三种做法:
- if 条件控制:制定拿筷子的规则,筷子奇偶限制
- 同步量限制:对进程加以限制,最多允许 $n-1$ 个人同时用餐
- 互斥量限制:规定仅当左右两只筷子同时可用时才进餐
3.实现
同时拿起筷子:当同时都拿起左筷子或同时都拿起右筷子,可能会造成死锁
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| semaphore chopsticks[n];
void init() {
for (int i = 0; i < n; i++)
chopsticks[i] = 1;
}
void philosopher_i(int i) {
while (true) {
P(chopsticks[i]);
P(chopsticks[(i + 1) % n]);
吃饭;
V(chopsticks[i]);
V(chopsticks[(i + 1) % n]);
思考;
}
}
|
if 条件控制:奇数号哲学家先拿左边筷子,偶数号哲学家先拿右边筷子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
| semaphore chopsticks[n];
void init() {
for (int i = 0; i < n; i++)
chopsticks[i] = 1;
}
void philosopher_i(int i) {
while (true) {
if (i % 2) {
P(chopsticks[i]);
P(chopsticks[(i + 1) % n]);
吃饭;
V(chopsticks[i]);
V(chopsticks[(i + 1) % n]);
思考;
} else {
P(chopsticks[(i + 1) % n]);
P(chopsticks[i]);
吃饭;
V(chopsticks[(i + 1) % n]);
V(chopsticks[i]);
}
}
}
|
同步量限制:即限制进餐人数,最多允许 $n-1$ 个人同时用餐
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| semaphore chopsticks[n];
semaphore num = 4;
void init() {
for (int i = 0; i < n; i++)
chopsticks[i] = 1;
}
void philosopher_i(int i) {
while (true) {
P(num);
P(chopsticks[i]);
P(chopsticks[(i + 1) % n]);
吃饭;
V(chopsticks[i]);
V(chopsticks[(i + 1) % n]);
V(num);
思考;
}
}
|
互斥量限制:规定仅当左右两只筷子同时可用时才进餐
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| semaphore chopsticks[n];
semaphore mutex = 1;
void init() {
for (int i = 0; i < n; i++)
chopsticks[i] = 1;
}
void philosopher_i(int i) {
while (true) {
P(mutex);
P(chopsticks[i]);
P(chopsticks[(i + 1) % n]);
V(mutex);
吃饭;
V(chopsticks[i]);
V(chopsticks[(i + 1) % n]);
思考;
}
}
|


