【概述】
在 关系操作 中,简单介绍了关系模型中的常用操作和关系查询语言,目前,在关系数据库领域,SQL 是最常用的关系数据语言,其是以关系代数为核心的,本篇将对关系代数进行简单介绍
关系代数是一种抽象的关系数据语言,其通过代数运算方式表示关系查询,所谓代数运算,是将一定的运算符作用于一定的运算对象上,通过形成表达式以得到预期的运算结果,所以运算对象、运算符、运算结果是代数运算的三大要素
关系代数的运算对象、运算结果都是关系,运算符分为集合运算符、专门的关系运算符两类,关系代数运算符如下表所示
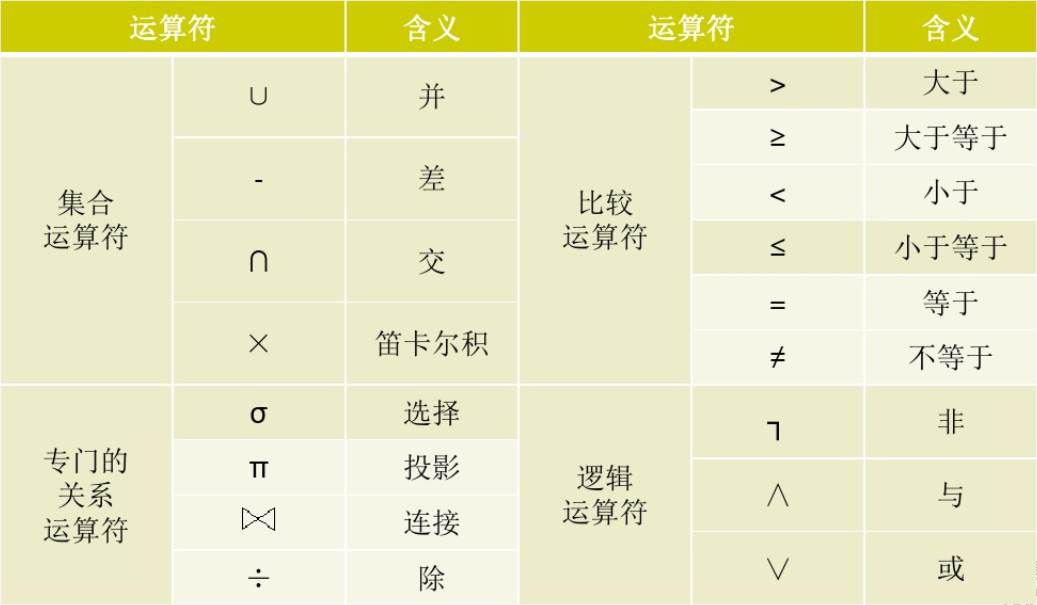
依据运算符的不同,关系代数的运算分为传统的集合运算、专门的关系运算
传统的集合运算将关系看成元组的集合,其运算是从关系的水平方向(以行的角度)进行;专门的关系运算不仅涉及到行,还涉及到列,在进行运算时,常涉及到比较运算符、逻辑运算符来辅助运算
【传统的集合运算】
传统的集合运算是二目运算,包括:并(Union)、差(Except)、交(Intersection)、笛卡尔积(Cartesian Product)四种运算
设关系 $R$ 和关系 $S$ 具有相同的目 $n$(两个关系都有 $n$ 个属性),且相应属性取自同一域,$t$ 是元组变量,$t \in R$ 表示 $t$ 是 $R$ 的一个元组,据此可以定义并、差、交三种运算
关系 $R$ 与 $S$ 的并仍是 $n$ 目关系,由属于 $R$ 或属于 $S$ 的元组组成,记作:
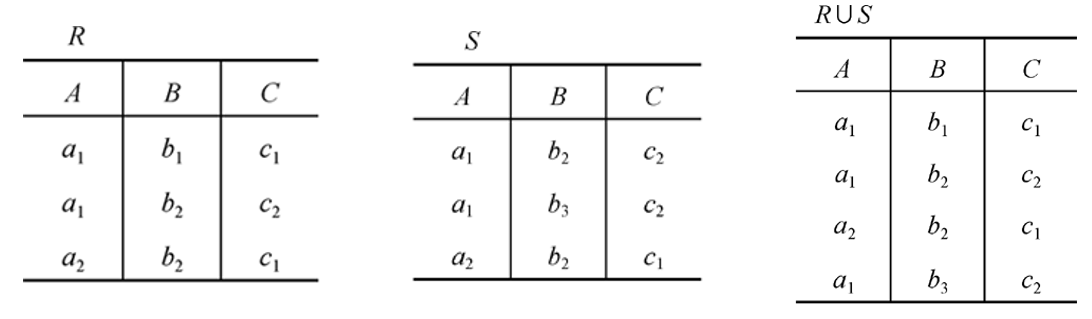
关系 $R$ 与 $S$ 的差仍是 $n$ 目关系,由属于 $R$ 但不属于 $S$ 的元组组成,记作:
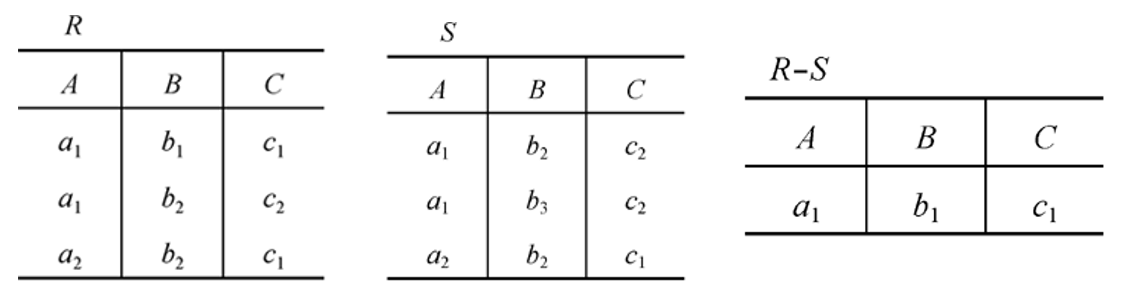
关系 $R$ 与 $S$ 的交仍是 $n$ 目关系,由既属于 $R$ 又不属于 $S$ 的元组组成,记作:
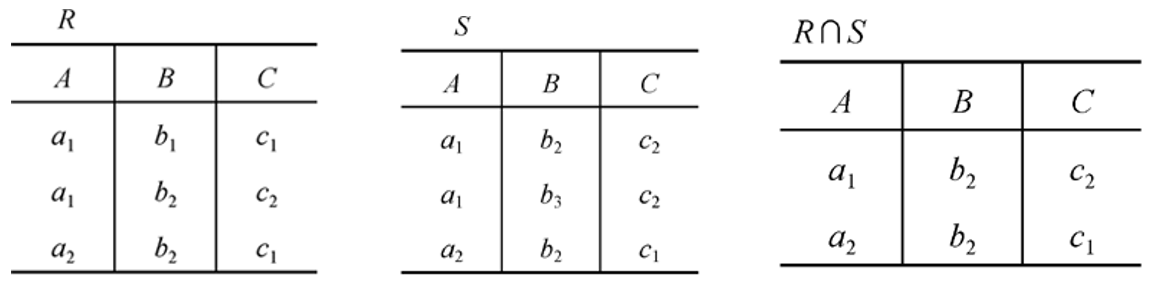
此外,关系的交可以用关系的差来表示,即:$R \cap S=R-(R-S)$
而关系的笛卡尔积的元素是元组,因此严格来讲其实是广义的笛卡尔积(Extended Cartesian Product),关于笛卡尔积详见:点击这里
设 $R$ 为 $n$ 目关系,$S$ 为 $m$ 目关系,有 $t_r \in R,t_s \in S$,关系 $R$ 与关系 $S$ 的笛卡尔积是一个 $n+m$ 列的元组的集合,记作:
其中,$\overset{\frown }{t_r t_s}$ 被称为元组的连接(concatenatoin),是一个 $n+m$ 列的元组,该元组的前 $n$ 列是关系 $R$ 的一个 $n$ 元组,后 $m$ 列是关系 $S$ 的一个 $m$ 元组
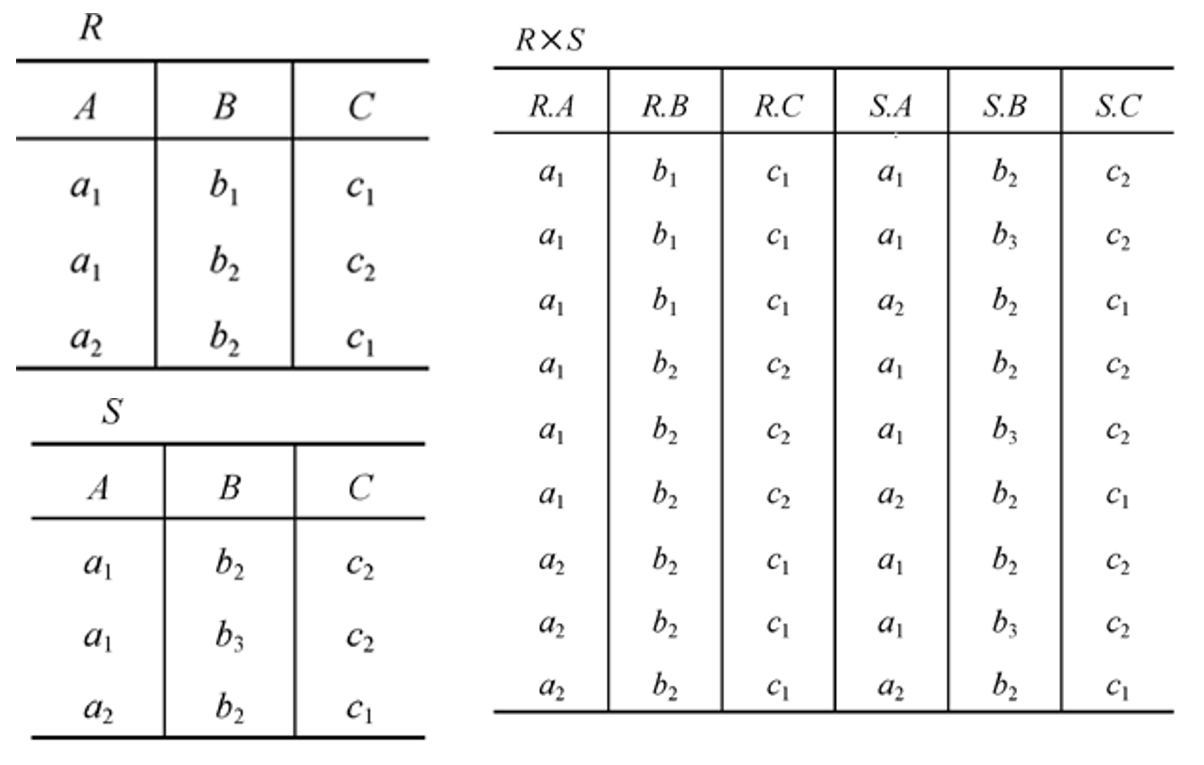
同时,在上例中可以看出,若 $R$ 有 $k_1$ 个元组,$S$ 有 $k_2$ 个元组,则关系 $R$ 和 $S$ 的笛卡尔积有 $k_1*k_2$ 个元组
【专门的关系运算】
引入
专门的关系运算包括选择、投影、连接、除运算等,为了叙述上的方便,引入以下记号:
设关系模式为 $R(A_1,A_2,…,A_n)$,其中的某个关系为 $R$,用 $t \in R$ 表示 $t$ 是 $R$ 的一个元组,$t[A_i]$ 表示元组 $t$ 中相应属性 $A_i$ 的一个分量
若 $A=\{A_{i1},A_{i2},…,A_{ik}\}$ 其中的 $A_{i1},A_{i2},…,A_{ik}$ 是 $A_1,A_2,…,A_n$ 中的一部分,则称 $A$ 为属性列或属性组,用 $\overline{A}$ 表示 $\{A_1,A_2,…,A_n\}$ 中去掉属性组 $A$ 后剩余的属性组,用 $t[A]=(t[A_{i1}],t[A_{i2}],…,t[A_{ik}])$ 表示元组 $t$ 在属性组 $A$ 上诸分量的集合
同时,以下图的学生-课程数据库为例,包括学生关系 Student、课程关系 Course、选修关系 SC,以便对专门的关系运算进行举例
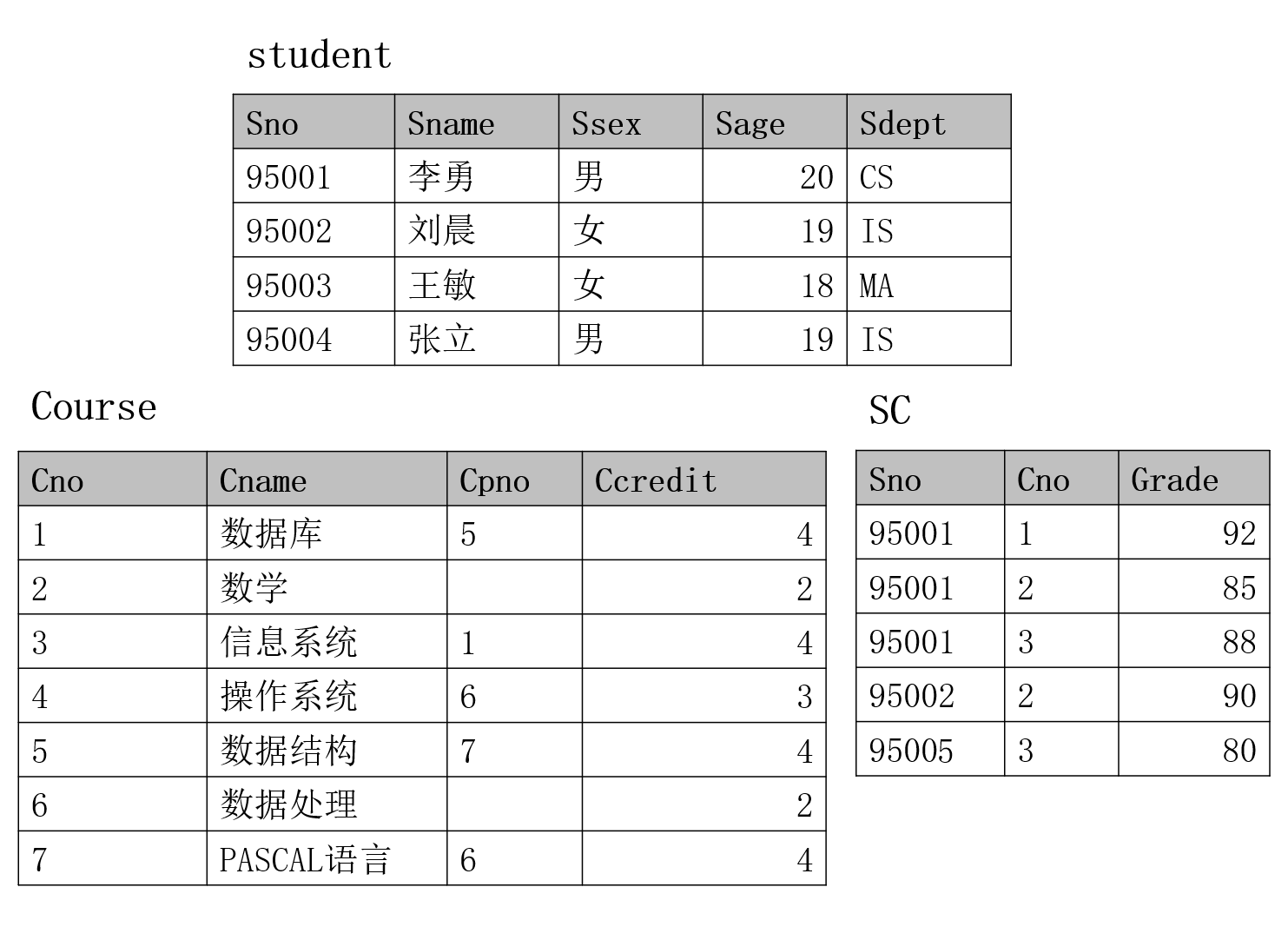
选择
选择(Selection)又称限制,其是在关系 $R$ 中选择满足给定条件的元组组成新的关系,记作:
其中,$F$ 表示选择条件,是一个逻辑表达式,取逻辑值 true 或 false,同时,在基本的选择条件上可以进一步的进行逻辑运算(与 $\wedge$、或 $\vee$、非 $\neg$)
逻辑表达式 $F$ 的基本形式为 $X_1 \theta Y_1$,其中 $\theta$ 代表比较运算符($>,<, \geq ,\leq ,\neq ,=$),$X_1$ 和 $Y_1$ 可代表属性名(也可用其序号代替)、常量、简单函数
综上所述,选择运算实际上是从关系 $R$ 中选取使逻辑表达式 $F$ 为 true 的元组,是从行角度进行的运算
例如,查询信息系(IS 系)全体学生:$\sigma_{Sdept=’IS\:’}(Student)$,结果如下
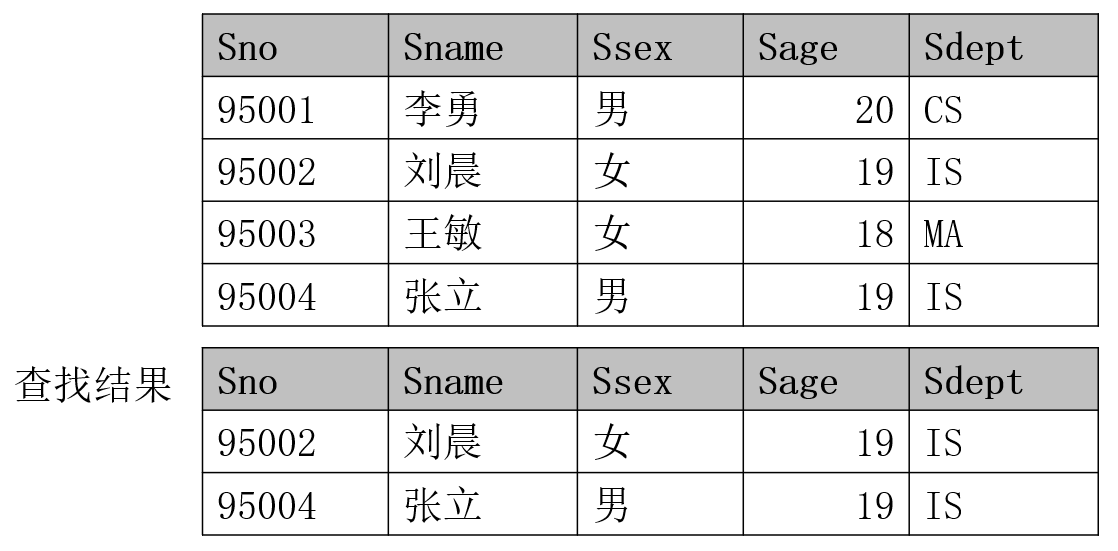
再例如,查询年龄大于等于 20 岁的男学生:$\sigma_{Sage\geq 20 \wedge Ssex=’男\:’}(Student)$,结果如下
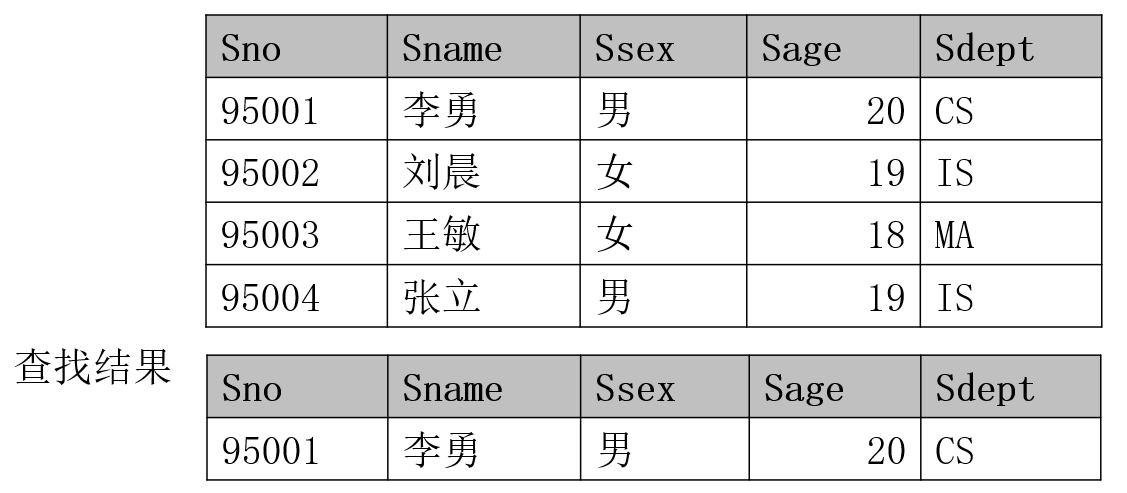
投影
投影(Projection)是在关系 $R$ 上选择若干属性列组成新的关系,记作:
其中,$A$ 为 $R$ 中的属性列
投影操作是对列进行运算的,但值得注意的是,投影后不仅取消了原关系中的某些列,而且可能取消某些元组,因为取消了某些列后,可能会出现重复的行,此时应该对完全相同行去重
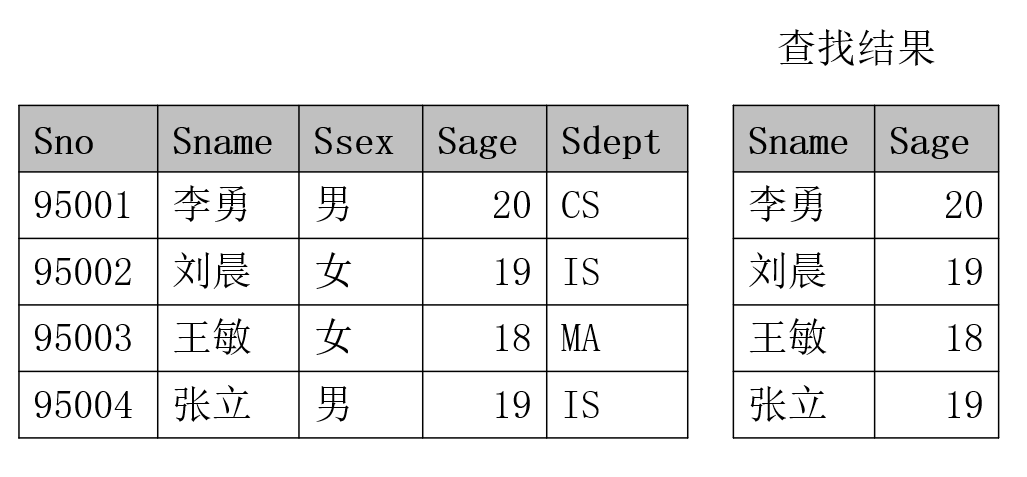
例如,查询所有学生的姓名和年龄:$\Pi_{Sname,Sage}(Student)$,结果如下
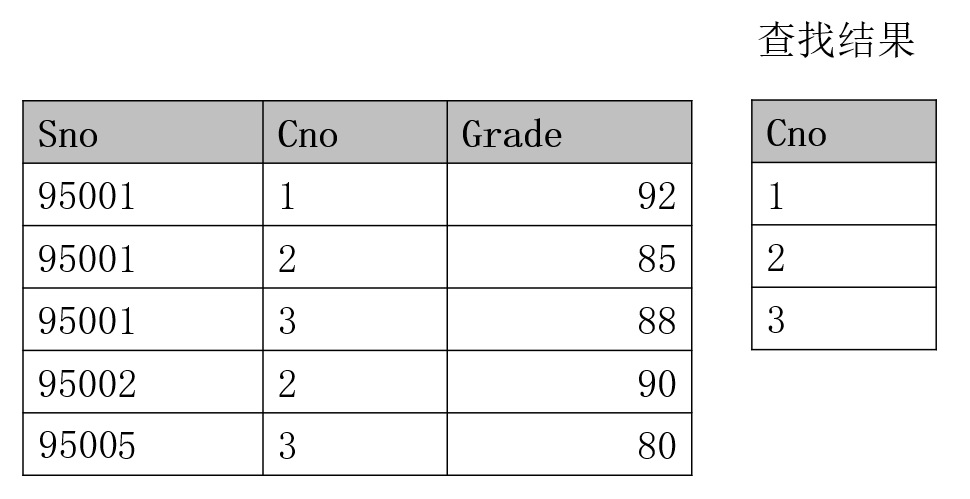
再例如,查询学号为 95001 号学生所选修的课程号:$\Pi_{Cno}(\sigma_{Sno=95001(SC)})$,结果如下
连接
定义
连接(Join)也称 $\theta$ 连接,是从两个关系 $R$ 与 $S$ 的笛卡尔积中选取属性间满足一定条件的元组组成新的关系,记作:
其中,$A$ 和 $B$ 分别为关系 $R$ 和 $S$ 上目(列数)相等且可比的属性组,$\theta$ 为比较运算符
该运算式实质为:在 $R$ 和 $S$ 的笛卡尔积 $R \times S$ 中选取 $R$ 关系在 $A$ 属性组上的值与 $S$ 关系在 $B$ 属性组上的值满足比较关系 $\theta$ 的元组
等值连接与自然连接
连接运算中最常用的连接有两种,一种是等值连接(Equijion),另一种是自然连接(Natural join),除这两种连接外的所有连接,都称为非等值连接
等值连接是指当比较运算符 $\theta$ 为 $=$ 时的连接运算,其是从关系 $R$ 和 $S$ 的笛卡尔积中选取 $A$、$B$ 属性组的属性值相等的元组组成新的关系,即:
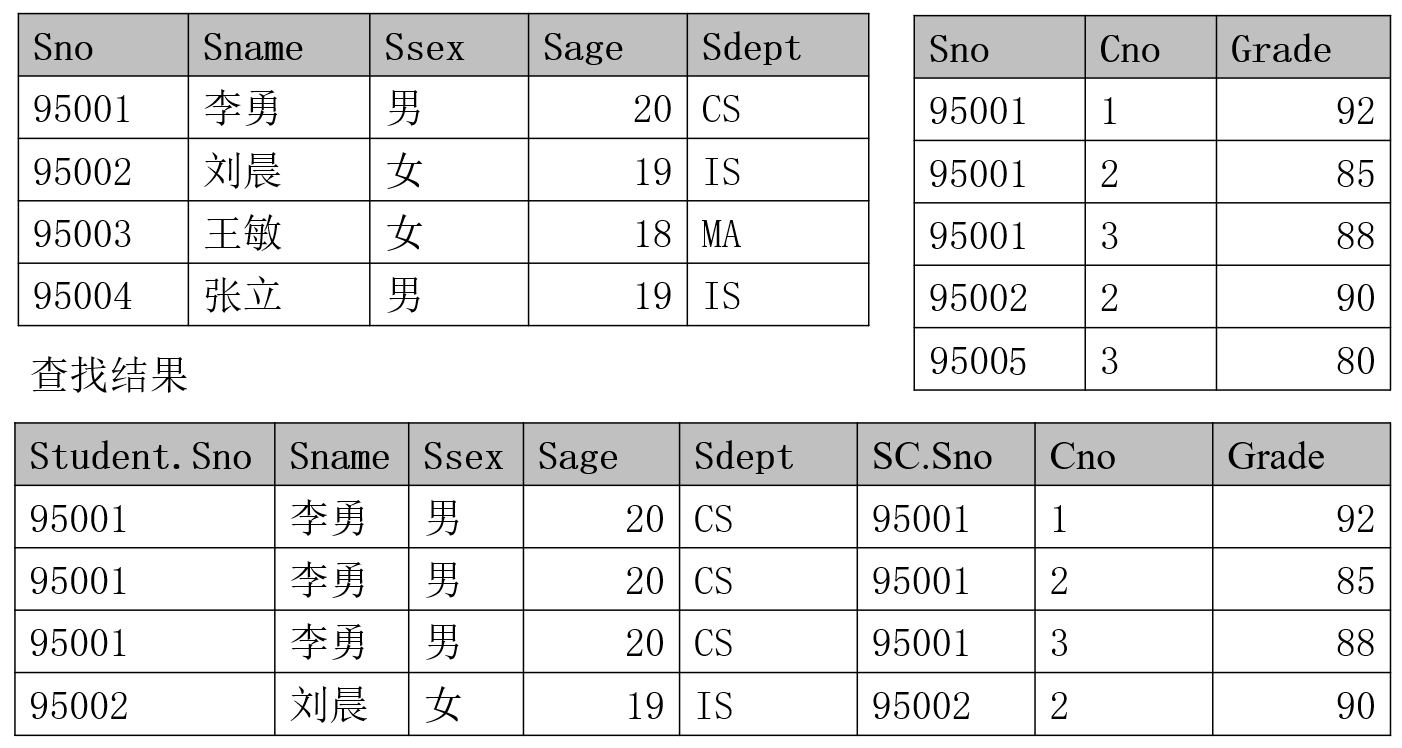
例如,学生关系 Student 和选修关系 SC 的学号属性 Sno 的等值连接 $Student \underset{Student.Sno=Sc.Sno}{\bowtie} SC$,结果如下
自然连接是一种特殊的等值连接,其要求两个关系中进行比较的分量必须是同名的属性组,并且在结果中将重复的属性列去掉,即:
其中,$U$ 为关系 $R$ 和 $S$ 的全体属性的集合
可以发现,一般的连接操作是从行的角度进行运算,而自然连接由于要取消重复列,其是同时从行和列的角度进行运算
此外,值得注意的是,当 $R$ 与 $S$ 无相同属性时,$R\bowtie S=R\times S$
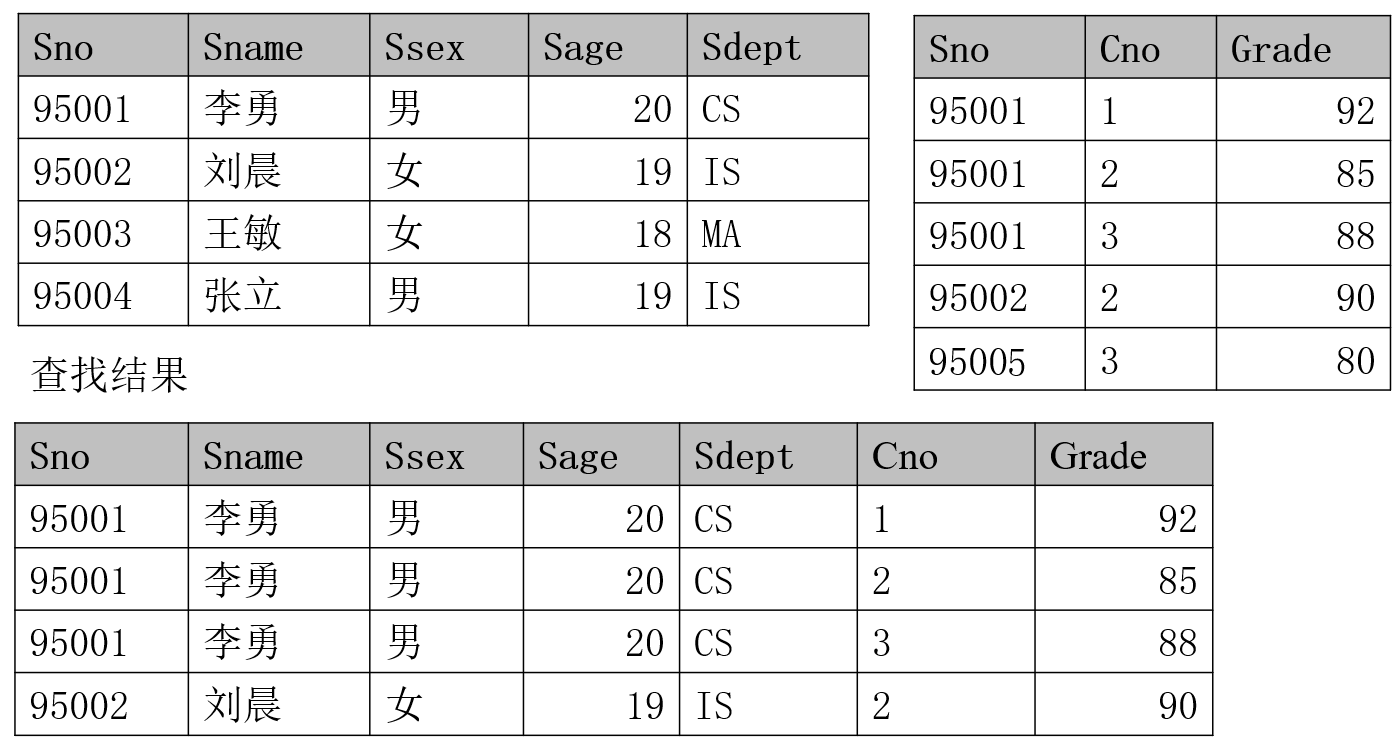
例如,学生关系 Student 和选修关系 SC 作自然连接 $Student \bowtie SC$,结果如下
悬浮元组与外连接
当两个关系 $R$ 与 $S$ 作自然连接时,选择两个关系在公共属性上值相等的元组构成新的关系,此时,关系 $R$ 中某些元组可能在 $S$ 中不存在公共属性值相等的元组,使得 $R$ 中这些元组在操作时被舍弃了,同样,$S$ 中的某些元组也可能被舍弃,这些被舍弃的元组称为悬浮元组(Dangling tuple)
例如,对学生关系 Student 和选修关系 SC 的自然连接 $Student \bowtie SC$ 中,学生关系 Student 的第 3 个、第 4 个元组,选修关系的第 5 个元组,就是悬浮元组

如果把悬浮元组也保存在结果关系中,在其他属性上填上空值(NULL),那么这种连接就叫外连接(Outer join),记作:$R \Join S$
例如,学生关系 Student 和选修关系 SC 的外连接 $Student \bowtie SC$,结果如下
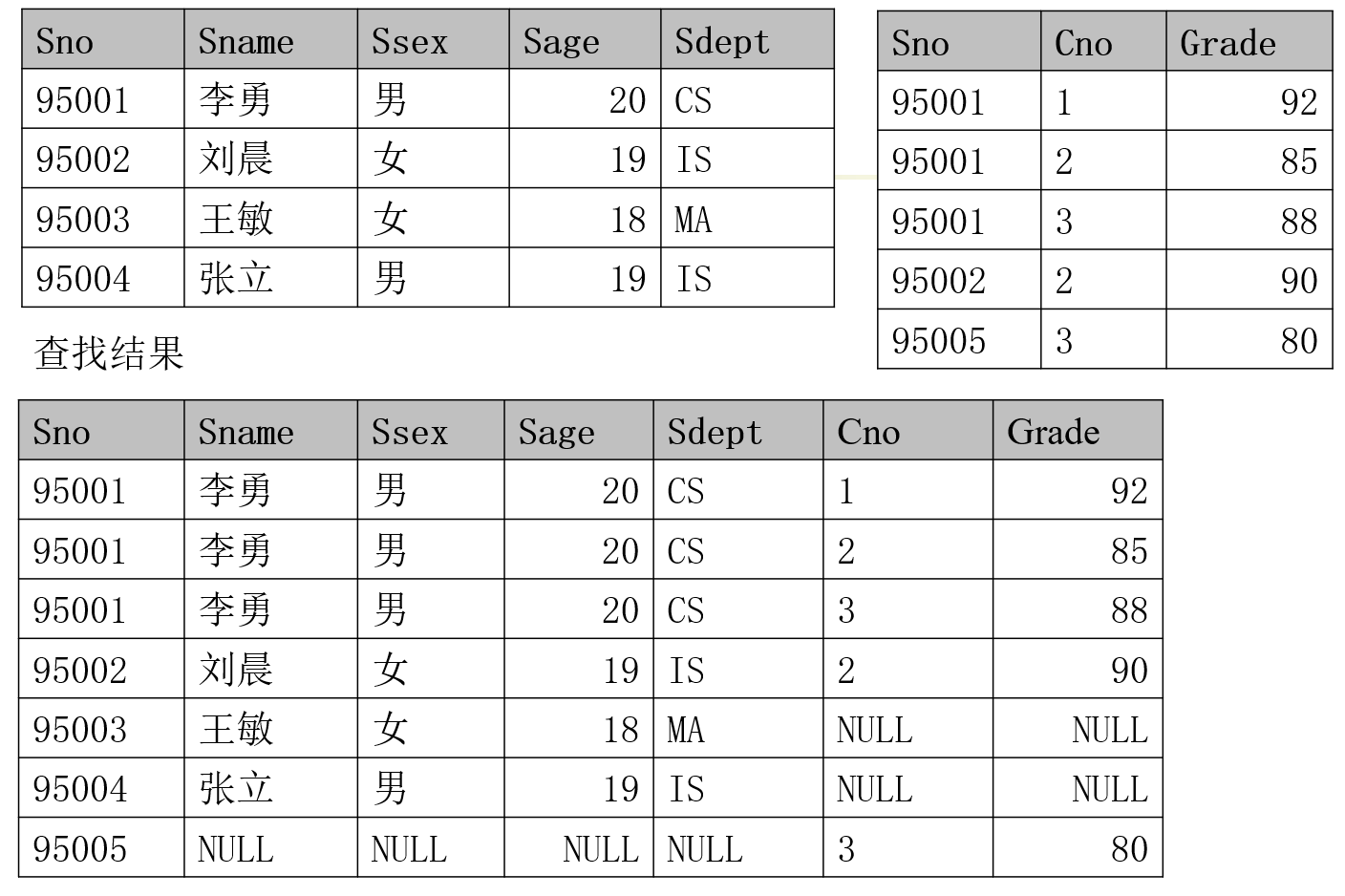
如果只保留左边关系 $R$ 中的悬浮元组,那么这种连接就叫左外连接(Left join),记作:$R \rtimes S$
例如,学生关系 Student 和选修关系 SC 的左外连接 $Student \bowtie SC$,结果如下
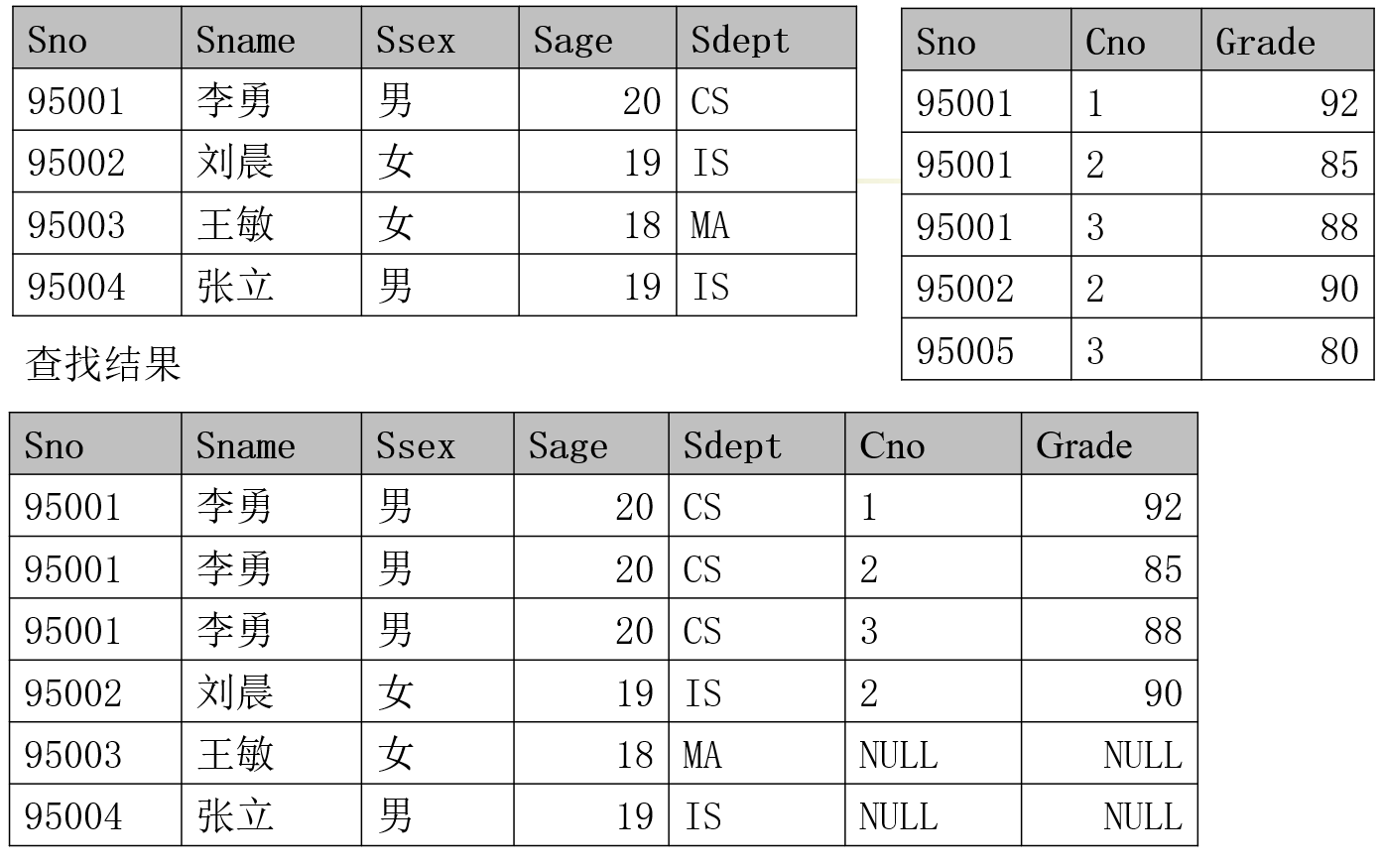
如果只保留左边关系 $R$ 中的悬浮元组,那么这种连接就叫右外连接(Right join),记作:$R \ltimes S$
例如,学生关系 Student 和选修关系 SC 的右外连接 $Student \bowtie SC$,结果如下
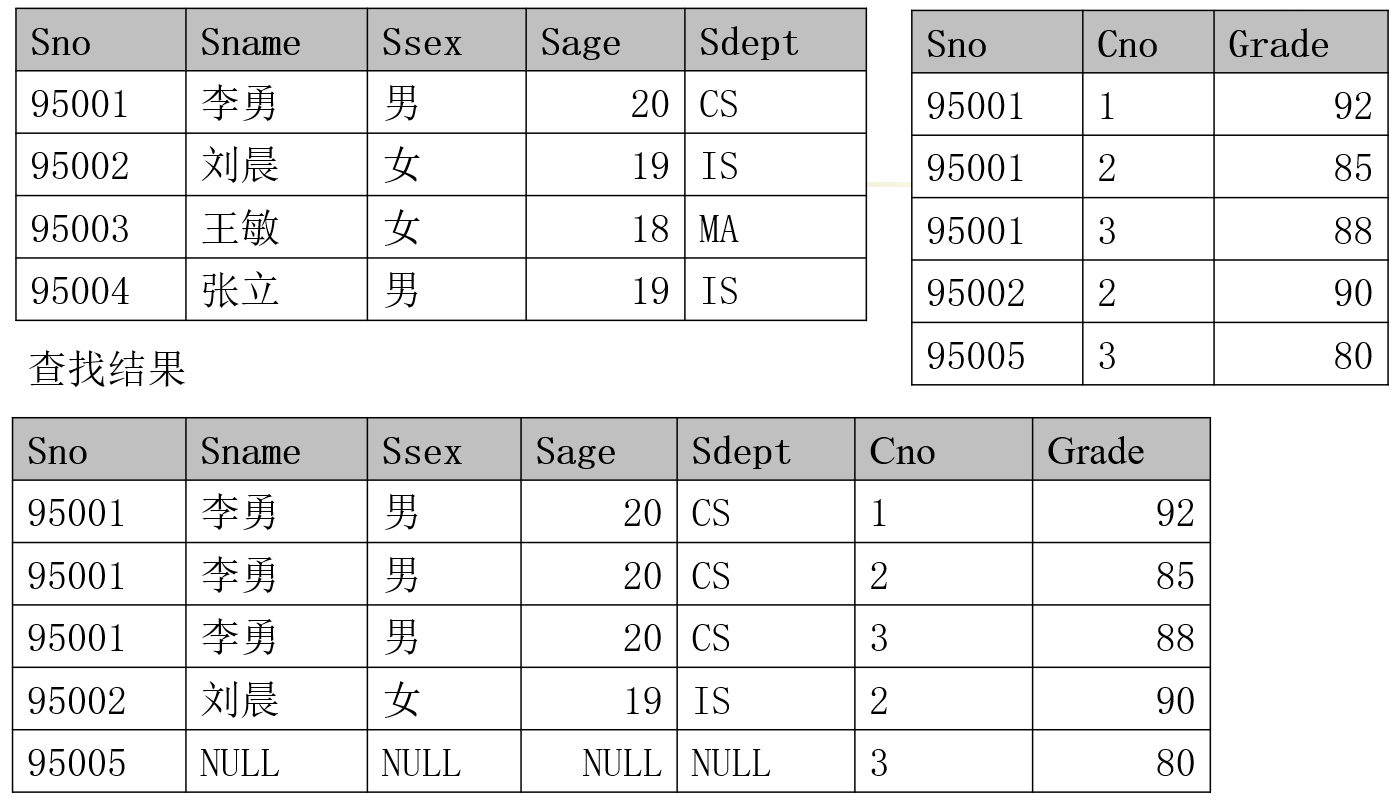
除运算
象集
对于给定一个关系 $R(X,Z)$,其中 $X$ 和 $Z$ 为属性组,当 $t[X]=x$ 时,定义 $x$ 在 $R$ 中的象集(Images set)为:
其表示在关系 $R$ 中,选出属性组 $X$ 上所有取值为 $x$ 的元组,去掉这些元组的属性组 $X$ 上的分量,只保留这些元组的属性组 $Z$ 上的分量
例如,对于如下的姓名课程关系,取 x=张军,象集 $Z_x$ 代表张军所选修的所有课程
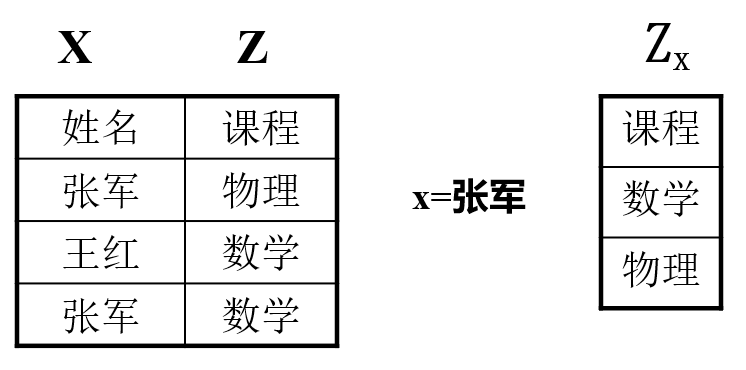
除运算
在有了象集的定义后,我们用象集来定义除运算(Division)
对于给定关系 $R(X,Y)$ 和 $S(Y,Z)$,其中 $X$、$Y$、$Z$ 为属性组,$R$ 中的 $Y$ 和 $S$ 中的 $Y$ 可以有不同属性名,但必须出自相同的域
关系 $R$ 与关系 $S$ 进行除运算,得到一个新的关系 $P(X)$,$P$ 是 $R$ 中满足下列条件的元组在 $X$ 属性列上的投影:元组在 $X$ 的分量值 $x$ 的象集 $Y_x$ 包含关系 $S$ 在 $Y$ 上的投影的集合
记作:
其中,$x=t_r[X]$,$Y_x$ 为 $x$ 在关系 $R$ 中的象集
简单来说,设关系 $R$ 除以关系 $S$ 的结果为关系 $T$,则 $T$ 包含所有在 $R$ 但不在 $S$ 中的属性及其值,且 $T$ 的元组与 $S$ 的元组的所有组合都在 $R$ 中
举例来说,假设关系 $R$ 和关系 $S$ 如下
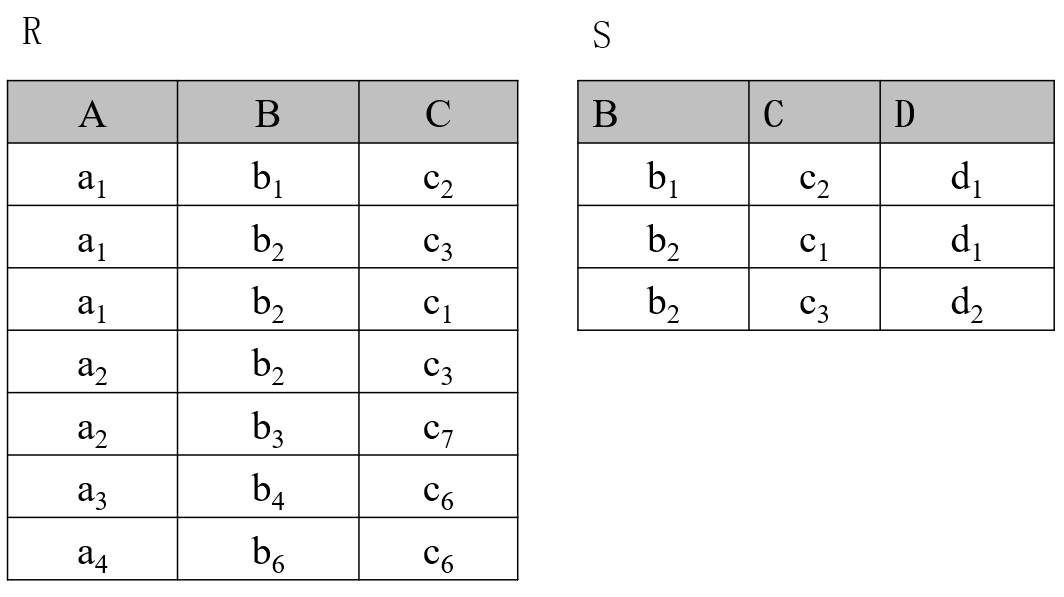
在关系 $R$ 中,属性 $A$ 可取的值为 $\{a_1,a_2,a_3,a_4\}$,则这 4 个可取值的象集如下
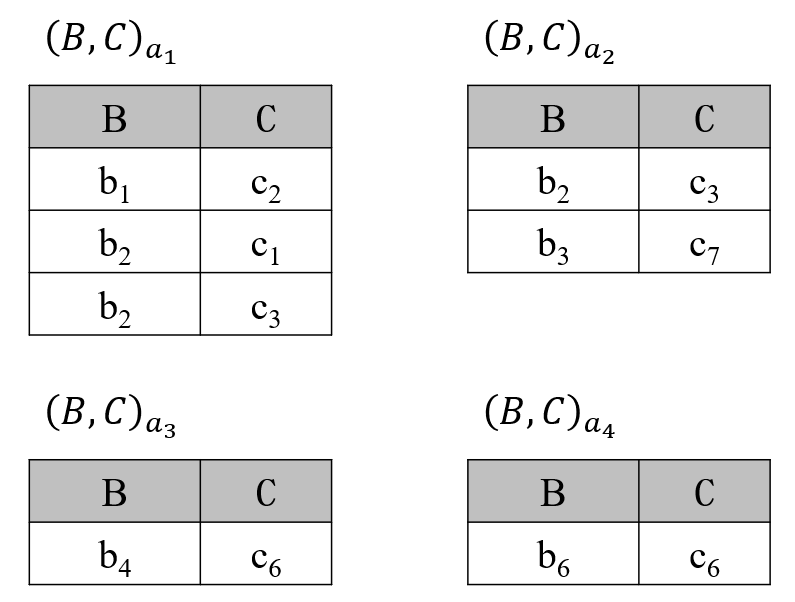
关系 $S$ 在属性组 $(B,C)$ 上的投影为
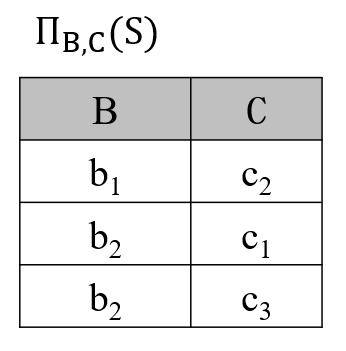
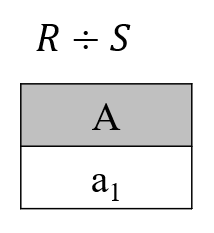
显然,只有 $a_1$ 的象集 $(B,C)_{a_1}$ 包含了 $S$ 在属性组 $(B,C)$ 上的投影,故 $R \div S$ 的结果如下
【关系代数表达式】
关系代数中,将关系代数运算经过有限次复合后形成的表达式,称为关系代数表达式
在表达式中,关系代数运算的结果没有可供引用的名字,这使得复杂的查询显得非常冗长
为解决这个问题,引入了命名运算,将一个名字赋给关系代数表达式,记作:
其中,$E$ 为给定的关系代数表达式,$x$ 表示名字
命名运算除了赋名外,还可以设置关系代数表达式各属性的名字
假设关系代数表达式 $E$ 是 $n$ 元的,则表达式:$\rho_{x(A_1,A_2,…,A_n)}(E)$ 返回表达式 $E$ 的结果,并赋名为 $x$,同时将 $E$ 的各属性更名为 $A_1,A_2,…,A_n$

