Alex_McAvoy

想要成为渔夫的猎手

Matlab 数据可视化

发表于 分类于
本文字数： 11k 阅读时长 ≈ 10 分钟

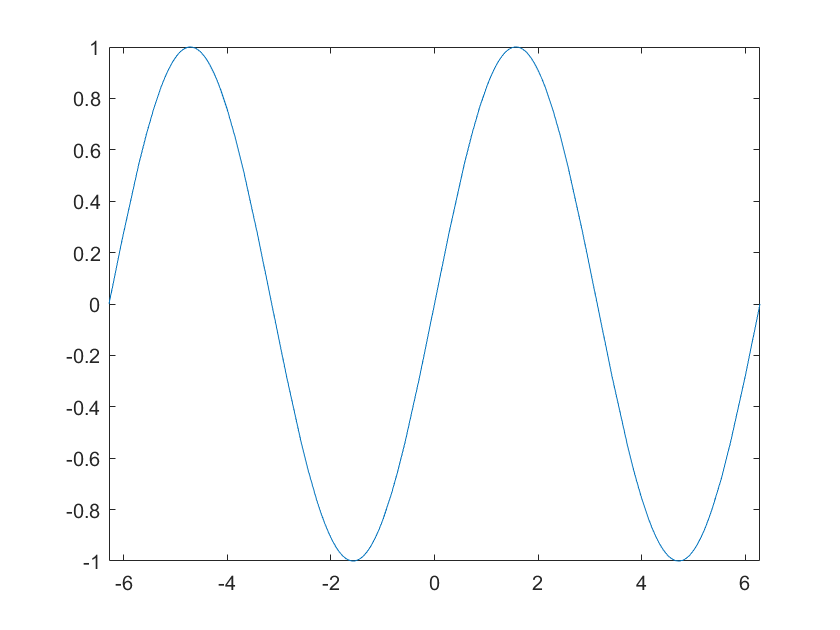
【图形绘制流程】

  1. 数据准备：产生采样自变量，计算相应函数值向量
  2. 选定图形窗口与子图
  3. 调用绘图函数
  4. 设置坐标轴、刻度、网格
  5. 设置线性、标记类型、粗细
  6. 添加图名、坐标名、图例
  7. 导出

【画布与子图】

子图

matlab 中，画布默认从 figure1 开始，导出的图形依次为：figure.1、figure.2…

因此一般画图时，直接利用 figure 新建画布即可

1
2
>> figure   %新建画布
>> ...

若绘制了多个画布，想在不同的画布间进行切换时，利用 figure(k) 即可完成画布切换

1
2
3
4
>> figure(2) % 切换到画布2
>> ...
>> figure(1) % 切换到画布1
>> ...

子图

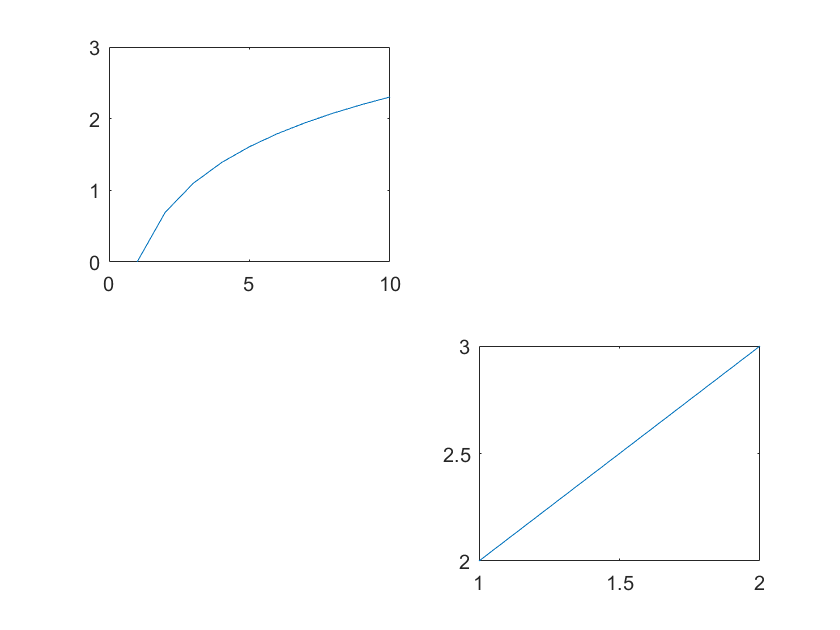
matlab 允许在同一画布下绘制多幅相互独立的子图，利用 subplot() 命令即可设置子图大小并切换绘制域

调用格式：subplot(n,m,k) 将画布分为 nm 大小，选中第 k 个*(行优先排序)作为当前绘制域

在调用 subplot() 后，所有的操作均在当前绘制域内完成，若想切换绘制域，再次调用 subplot() 即可

需要说明的是，在使用 subplot() 后，若想再绘制充满整个图形窗的图形时，利用 clf 命令进行清空即可

1
2
3
4
5
6
>> figure
>> subplot(2,1,1) % 在第1个子图进行绘制
>> ...
>> subplot(2,1,2) % 在第2个子图进行绘制
>> ...
>> subplot(2,1,1) % 在第1个子图进行绘制

实例：

1
2
3
4
5
6
7
8
>> figure
>> subplot(2,2,1)
>> plot(1:5)
>> subplot(2,2,4)
>> plot(2:3)
>> subplot(2,2,1)
>> plot(log(1:2))
>> plot(log(1:10))

【二维图形】

散点图与曲线图

基本使用

利用 plot() 函数即可完成散点图和连线图的绘制：

plot(x,y)：以 x 为横坐标，y 为纵坐标，有序绘制曲线

1
2
3
4
>> figure
>> x=0:0.05:5;
>> y=log(x);
>> plot(x,y)

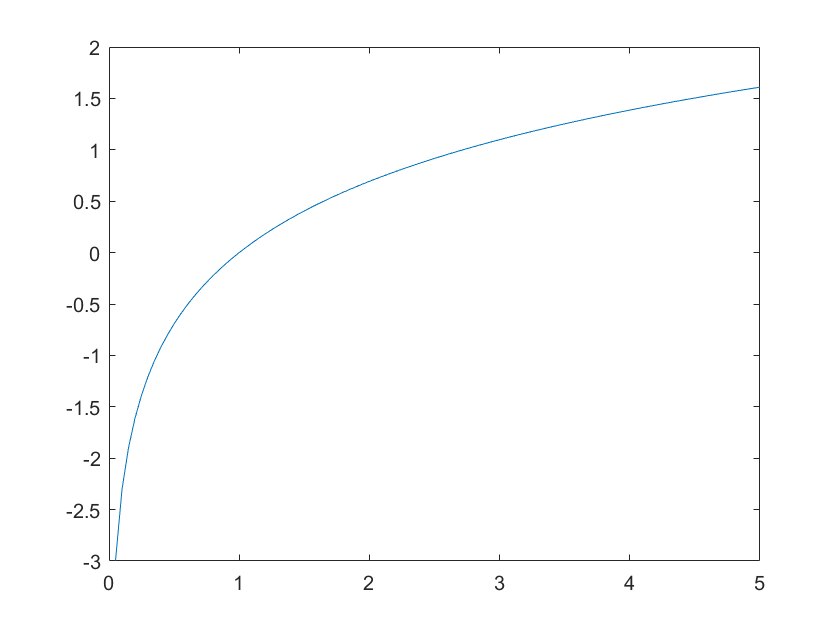
plot(x,y,'o')：以 x 为横坐标，y 为纵坐标，有序绘制散点图

1
2
3
4
>> figure
>> x=0:0.5:5;
>> y=log(x);
>> plot(x,y)

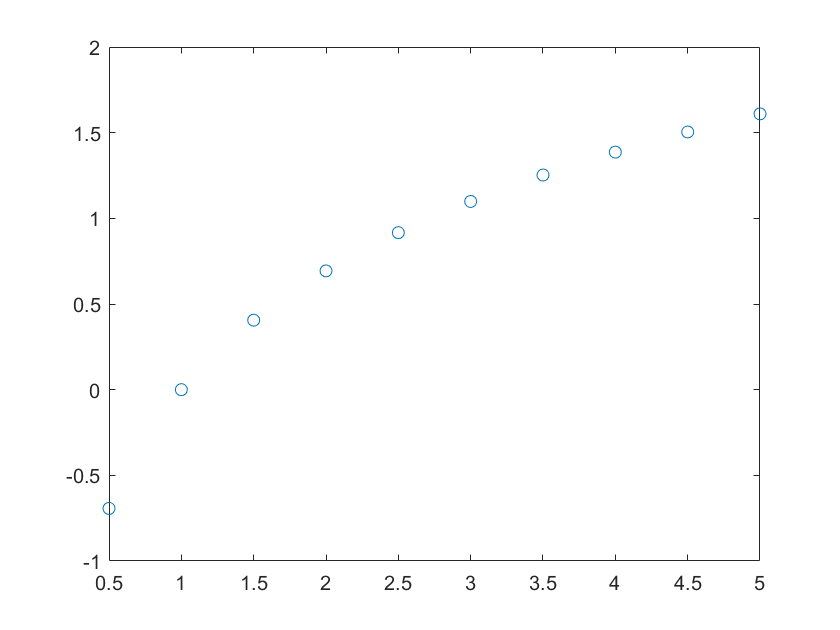
plot(y)：以 1:n 为横坐标，y 为纵坐标，有序绘制曲线，其中 n 是数组 y 的长度

1
2
3
>> figure
>> y=0:0.05:5;
>> plot(y)

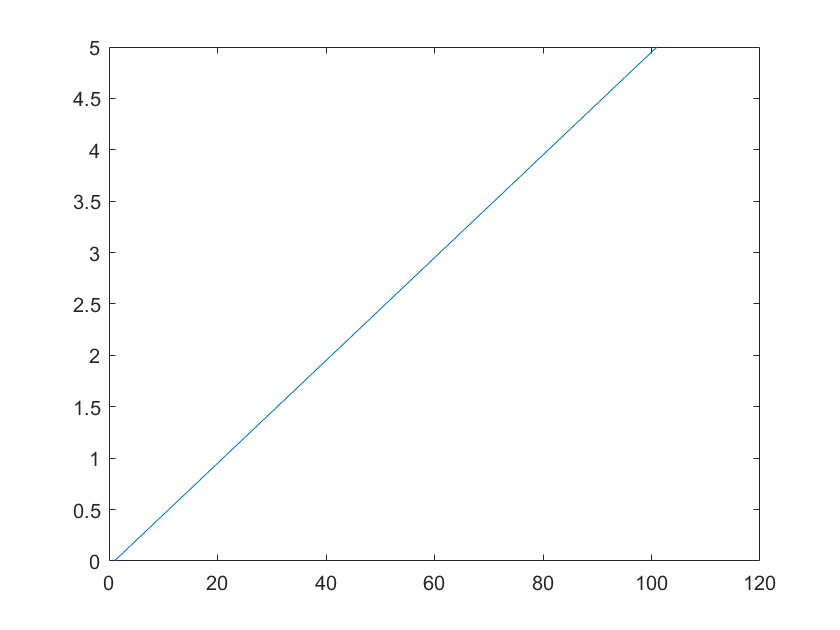
plot(z)：以横轴为实轴，纵轴为虚轴，在复平面上绘制有序集合

1
2
3
>> figure
>> z=[1+2i,3+4i,5+55i,45+4i];
>> plot(z,'o','MarkerFaceColor','b')

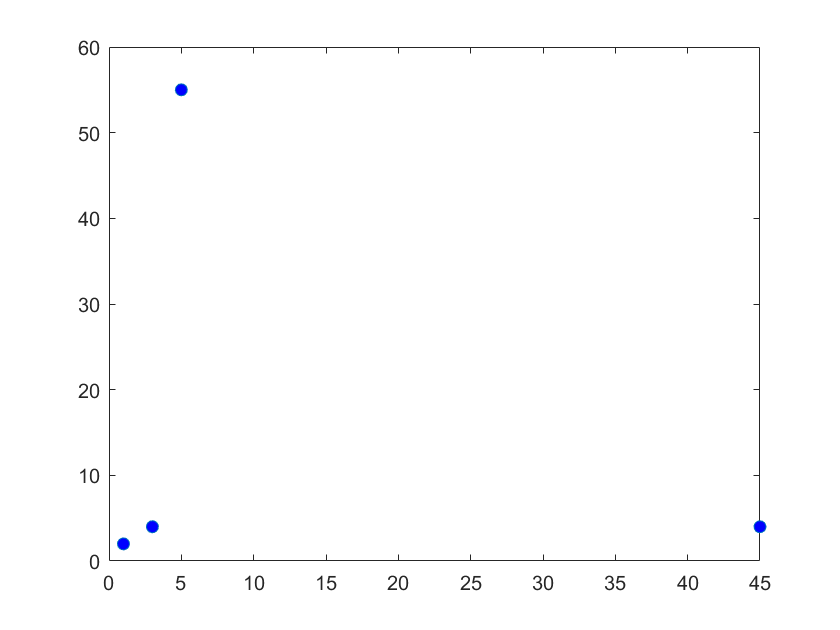
线型、标记、颜色

用法：plot(x,y,'str')：

颜色：在绘制多个图形时，matlab 会自动分配颜色，但如果对分配的颜色不满意，可以自己指定

str 颜色
r 红色
m 粉红
g 绿色
c 青色
y 黄色
k 黑色

线型

str 线型
‘-‘ 实线
‘—‘ 虚线
‘:’ 点线
‘-.’ 点划线

标记点

str 标记 str 标记
. 点 s 正方形
^ 上三角 > 右三角
v 下三角 < 左三角
+ +号 p 五角星
* 星号 h 六角星
d 菱形 o 空心圆

注：选项可以连在一起用，如:-.g表示绘制绿色的点划线，g+ 表示用绿色的 + 号绘制曲线

例如：plot(x,y,'+-r')：将散点图的每个点的大小指定为 n

1
2
3
4
>> figure
>> x=0:0.5:5;
>> y=log(x);
>> plot(x,y,'+-r')

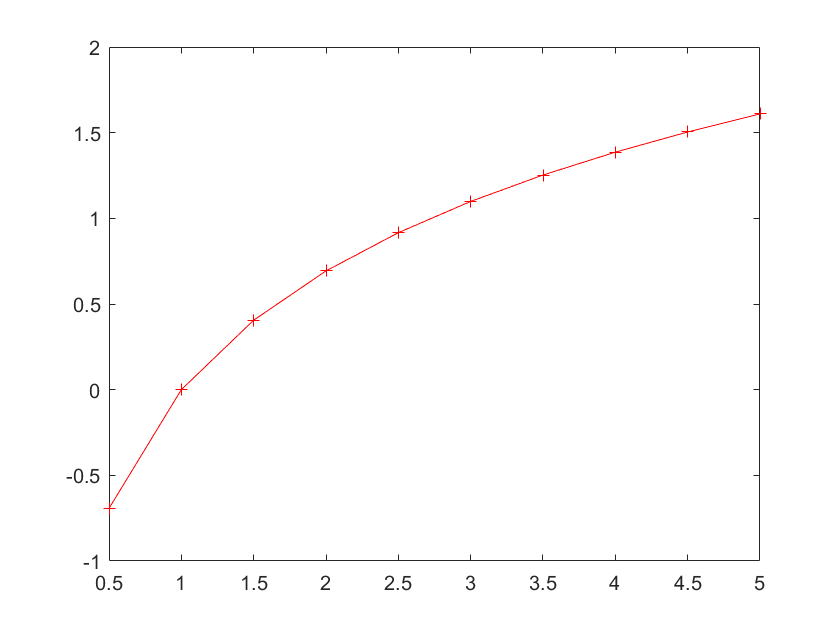
线型粗细

plot(x,y,'o','MarkerSize',n)：将散点图的每个点的大小指定为 n

1
2
3
4
>> figure
>> x=0:0.5:5;
>> y=log(x);
>> plot(x,y,'o','MarkerSize',15)

plot(x,y,'LineSize',n)：将曲线图的线的大小指定为 n

1
2
3
4
>> figure
>> x=0:0.5:5;
>> y=log(x);
>> plot(x,y,'LineSize',15)

散点曲线图的颜色

当绘制散点与曲线的叠加时，有时希望将空心圆的散点填充，并使得两种颜色不同

例如：plot(x,y,'-ok','MarkerFaceColor','r')

1
2
3
4
>> figure
>> x=0:0.5:5;
>> y=log(x);
>> plot(x,y,'-ok','MarkerFaceColor','r')

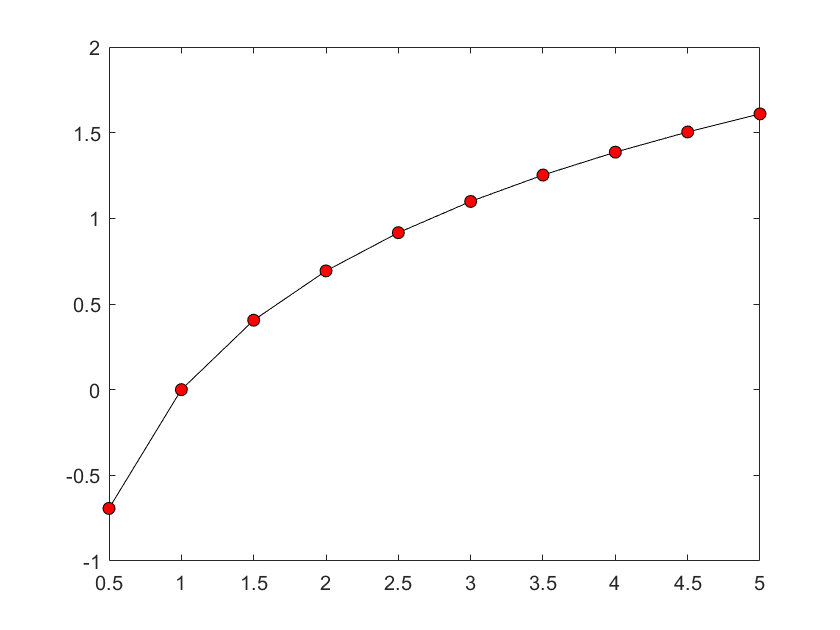
栅格

有时想要对当前图形开启栅格，可以利用 grid 命令

  • grid on：开启栅格
  • grid off：关闭栅格
  • grid：在开启/关闭间切换
1
2
3
4
5
>> figure
>> x=0:0.5:5;
>> y=log(x);
>> plot(x,y,'+-r')
>> grid on

图形叠绘

当有时需要在一张图形上画多个图形时，可利用 hold 命令来开启/关闭图形叠绘

  • hold on：开启图形叠绘
  • hold off：关闭图形叠绘
  • hold：在图形叠绘开启/关闭中切换
1
2
3
4
5
6
>> figure
>> x=0:0.5:5;
>> y=log(x);
>> hold on
>> plot(x,y)
>> plot(x,2*y)

3.2 散点图

scatter(x,y)：以 x、y 为坐标绘制散点图

scatter(x,y,'fill')：以 x、y 为坐标绘制散点图，并将散点填充

1
2
3
4
5
6
7
>> figure
>> x=rand(1,5);
>> y=rand(1,5);
>> subplot(1,2,1)
>> scatter(x,y)
>> subplot(1,2,2)
>> scatter(x,y,'fill')

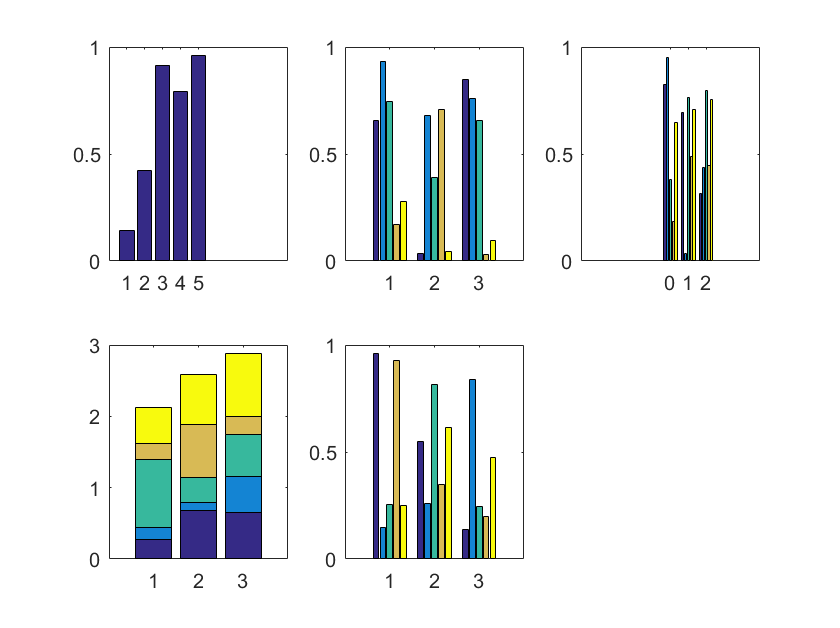
【柱状图】

matlab 中利用 bar() 来绘制柱状图，用垂直条形以表示向量或矩阵中的值

  • bar(x)：x 为向量时，为 x 中每一个元素画出柱状图；x 为矩阵时，将其分解为几个行向量，来画出柱状图
  • bar(x,y)：以严格单增的 x 向量为横坐标，将矩阵 y 分解成行向量，在指定的横坐标处画出，要求 x 的长度与 y 的行数相同
  • bar(x,'stacked')：以累计式绘出柱状图图
  • bar(x,'grouped')：以分组式绘出柱状图
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
>> figure
>> subplot(2,3,1)
>> x=rand(1,5);
>> bar(x)

>> subplot(2,3,2)
>> x=rand(3,5);
>> bar(x)

>> subplot(2,3,3)
>> x=0:2;
>> y=rand(3,5);
>> bar(x,y)

>> subplot(2,3,4)
>> x=rand(3,5);
>> bar(x,'stacked')

>> subplot(2,3,5)
>> x=rand(3,5);
>> bar(x,'grouped')

饼图

matlab 中利用 pie() 来绘制饼图，pie3() 来绘制 3D 饼图

  • pie(x)：绘制参数为 x 的饼图
  • pie(x,pos)：绘制参数为 x 的饼图，pos 为与 x 同维的矩阵，若其中有非 0 元素，则对应的扇区向外移一些
  • pie3(x)：绘制参数为 x 的 3D 饼图
  • pie3(x,pos)：绘制参数为 x 的 3D 饼图，pos 为与 x 同维的矩阵，若其中有非 0 元素，则对应的扇区向外移一些
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>> figure
>> subplot(2,2,1)
>> x=[1,2,3;4,5,6];
>> pie(x)

>> subplot(2,2,2)
>> x=[1,2,3,4,5,6];
>> pos=[1,0,1,0,0,0];
>> pie(x,pos)

>> subplot(2,2,3)
>> x=[1,2,3;4,5,6];
>> pie3(x)

>> subplot(2,2,4)
>> x=[1,2,3,4,5,6];
>> pos=[1,0,1,0,0,0];
>> pie3(x,pos)

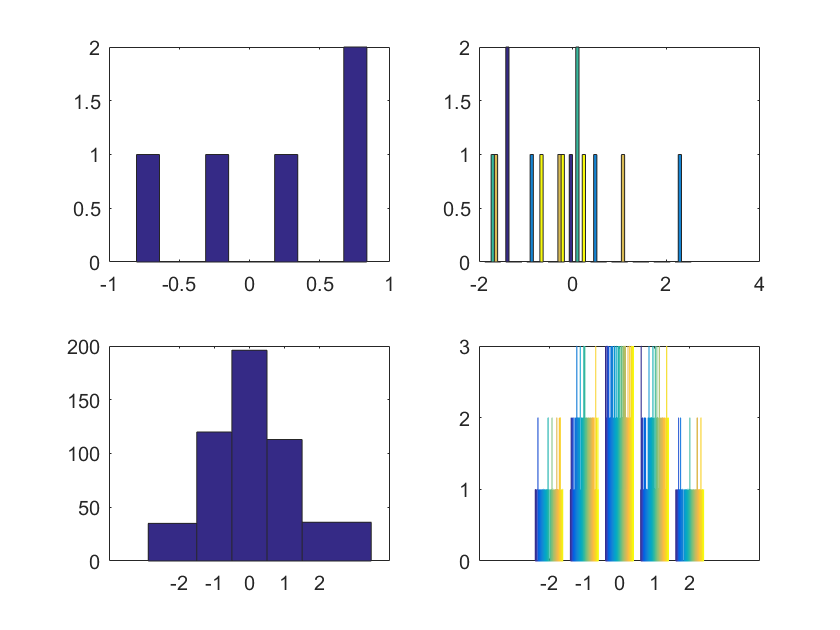
频数直方图

matlab 中利用 hist() 绘制二维条形直方图

  • hist(y)：将 y 中元素放在等距的 10 个条形中，且返回每个条形中的元素个数，当 y 为矩阵时，按列进行分解处理
  • hist(y,x)：以向量 x 为横轴，将 y 中元素放到 length(x) 个由 x 中元素指定的位置为中心的条形中
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>> subplot(2,2,1)
>> y=randn(1,5);
>> hist(y)

>> subplot(2,2,2)
>> y=randn(3,5);
>> hist(y)

>> subplot(2,2,3)
>> x=-2:2;
>> y=randn(1,500);
>> hist(y,x)

>> subplot(2,2,4)
>> x=-2:2;
>> y=randn(3,500);
>> hist(y,x)

【三维图形】

曲线图

在二维平面上，绘制曲线利用 plot() 函数，而在三维空间中，绘制曲线利用 plot3() 函数，该函数与 plot() 用法类似

  • plot3(X,Y,Z)
    • X、Y、Z 为同维向量时，绘制以 X、Y、Z 为 x、y、z 坐标的三维曲线
    • X、Y、Z 为同维矩阵时，绘制以 X、Y、Z 的对应列元素为 x、y、z 坐标的三维曲线
  • plot3(X1,Y1,Z1,X2,Y2,Z2)：绘制以 X1、Y1、Z1 和 X2、Y2、Z2 为 x、y、z 坐标的三维曲线

注：关于线型、标记、颜色等，见 3.二维图形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>> figure
>> subplot(2,2,1)
>> X=0:.1*pi:2*pi;
>> Y=cos(X);
>> Z=sin(X);
>> plot3(X,Y,Z)

>> subplot(2,2,2)
>> X=[0:.1*pi:2*pi;0:.1*pi:2*pi];
>> Y=cos(X);
>> Z=sin(X);
>> plot3(X,Y,Z,'o')

>> subplot(2,2,3)
>> plot3(0,0,0,4,5,6,'o')

网格图

对于函数 $z=f(x,y)$ 其三维网格图绘制过程如下：

  1. 确定自变量 x、y 的取值范围：x=x1:dx:x2,y=y1:dy:y2
  2. 构成 xoy 平面上的自变量采样格点矩阵：
    1. 利用格点矩阵原理生成：X=ones(size(y))*x,Y=y*ones(size(x))
    2. 利用 meshgrid() 函数生成：[X,Y]=meshgrid(x,y)
  3. 计算自变量采样格点上的函数值 $Z=f(x,y)$
  4. 利用 mesh() 函数绘图
    1. mesh(X,Y,Z)：以向量 X、Y 和矩阵 Z 绘制网格图
    2. mesh(Z)：以矩阵 Z 的列下标为 x 轴自变量，行下标为 y 轴自变量绘制网格图

注：关于线型、标记、颜色等，见 3.二维图形

1
2
3
4
5
6
7
8
9
10
11
>> figure
>> subplot(2,1,1)
>> x=-10:0.1:10;
>> y=-10:0.1:10;
>> [X,Y]=meshgrid(x,y); 
>> Z=X.^2+Y.^2;
>> mesh(X,Y,Z)

>> subplot(2,1,2)
>> [x,y,z]=peaks(25);
>> mesh(Z)

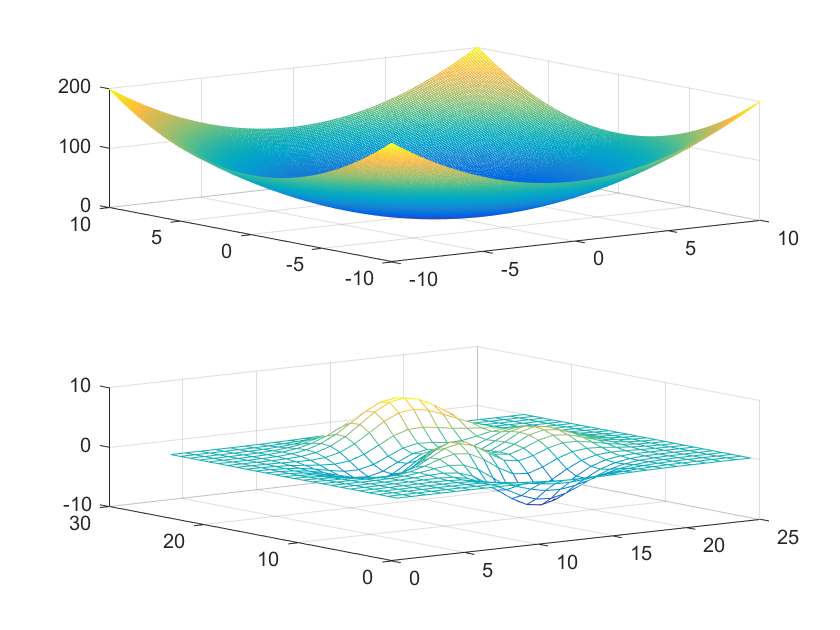
曲面图

对于函数 $z=f(x,y)$ 其三维曲面图与上述 4.2 网格图的绘制 相似，唯一的不同在于，网格图的绘制利用的是 mesh() 函数，而曲面图的绘制利用的是 surf() 函数

  • surf(X,Y,Z)：以向量 X、Y 和矩阵 Z 绘制曲面图

  • surf(Z)：以矩阵 Z 的列下标为 x 轴自变量，行下标为 y 轴自变量绘制曲面图

1
2
3
4
5
6
7
8
9
10
11
>> figure
>> subplot(2,1,1)
>> x=-10:0.1:10;
>> y=-10:0.1:10;
>> [X,Y]=meshgrid(x,y); 
>> Z=X.^2+Y.^2;
>> surf(X,Y,Z)

>> subplot(2,1,2)
>> [X,Y,Z]=peaks(25);
>> surf(Z)

光照图

在某些情况下，光照图能使图形表面差异更容易看到，其一般与曲面图组合使用

在 matlab 中，利用 camlight 等命令来设置光照

  • camlight left：设置光源在左侧
  • camlight rightt：设置光源在右侧
  • lighting phong：细化表面，使得光照效果更加平滑

在设置光照后，有时视角并不好，可以利用 view(a,b) 来改变视角，其中 a 代表方位角，b 代表仰角 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>> figure
>> subplot(2,1,1)
>> x=-10:0.1:10;
>> y=-10:0.1:10;
>> [X,Y]=meshgrid(x,y); 
>> Z=X.^2+Y.^2;
>> surf(X,Y,Z,'FaceColor','red','EdgeColor','none')
>> camlight left
>> lighting phong

>> subplot(2,1,2)
>> x=-10:0.1:10;
>> y=-10:0.1:10;
>> [X,Y]=meshgrid(x,y); 
>> Z=X.^2+Y.^2;
>> surf(X,Y,Z,'FaceColor','red','EdgeColor','none')
>> camlight left
>> lighting phong
>> view(2,50)

等值图

等值图即等高线图，在 matlab 中利用 contour() 命令即可完成绘制：

  • contour(X,Y,Z)：以向量 X、Y 和矩阵 Z 绘制等值图
  • contour(Z)：以矩阵 Z 的列下标为 x 轴自变量，行下标为 y 轴自变量绘制等值图
  • contour(X,Y,Z,n)：以向量 X、Y 和矩阵 Z 绘制等值图，n 为等值线条数
  • contour(Z,n)：以矩阵 Z 的列下标为 x 轴自变量，行下标为 y 轴自变量绘制等值图，n 为等值线条数
  • contour(Z,v)：以矩阵 Z 的列下标为 x 轴自变量，行下标为 y 轴自变量绘制等值图，v 为向量，向量长度为等值线条数，值为对应元素值
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
>> figure
>> subplot(2,2,1)
>> x=-10:0.1:10;
>> y=-10:0.1:10;
>> [X,Y]=meshgrid(x,y); 
>> Z=X.^2+Y.^2;
>> contour(X,Y,Z)

>> subplot(2,2,2)
>> x=-10:0.1:10;
>> y=-10:0.1:10;
>> [X,Y]=meshgrid(x,y); 
>> Z=X.^2+Y.^2;
>> contour(X,Y,Z,50)

>> subplot(2,2,3)
>> x=-10:0.1:10;
>> y=-10:0.1:10;
>> [X,Y]=meshgrid(x,y); 
>> Z=X.^2+Y.^2;
>> v=[1,2,3,4,5,6,7,8,9,10];
>> contour(Z,v)

>> subplot(2,2,4)
>> x=-10:0.1:10;
>> y=-10:0.1:10;
>> [X,Y]=meshgrid(x,y); 
>> Z=X.^2+Y.^2;
>> contour(Z,50)

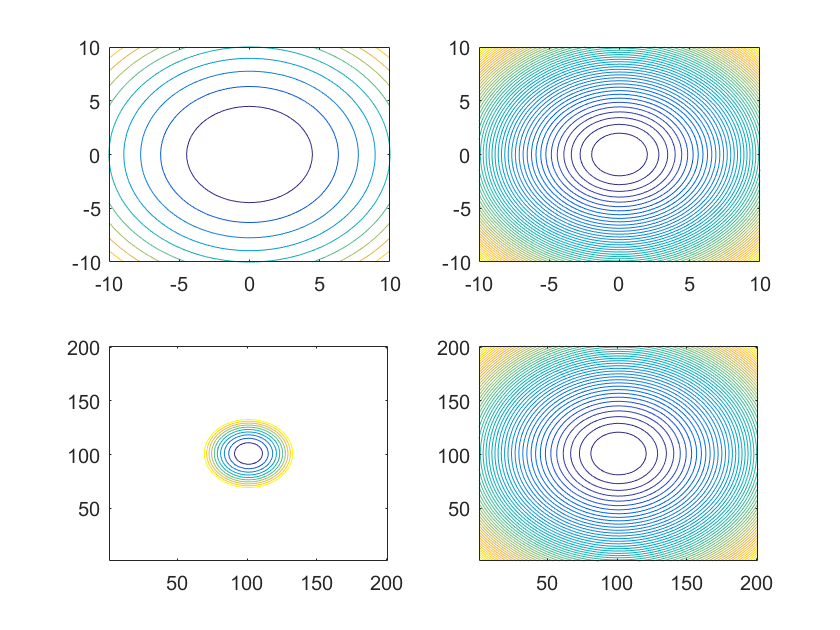
【四维图形】

囿于人类的局限性，对于四维图形难以想象，但在 matlab 中，可以用颜色来代表第四维，从而绘制四维图形

用 mesh() 和 surf() 绘制的图形，未给出颜色参数的情况下，其是沿着 z 轴变化的，但由于 z 轴已经存在，其不能提供新的信息，因此考虑利用颜色来描绘不受 3 个轴影响的某些属性。

1
2
3
4
5
6
7
8
9
>> figure
>> subplot(2,1,1)
>> [X,Y,Z]=peaks(25);
>> surf(X,Y,Z,Z)

>> subplot(2,1,2)
>> [X,Y,Z]=peaks(25);
>> R=X.^2+Y.^2;
>> surf(X,Y,Z,R)

【文字说明】

无论何种图形，均需要文字说明，图形窗口中常见的文字说明有：标题、坐标轴名、图例

标题与坐标轴名

  • title(str,'FontSize',num)：图片标题设为 str，字体大小为 num，默认为 11
  • xlabel(str,'FontSize',num)：x 坐标轴名设为 str，字体大小为 num，默认为 11
  • ylabel(str,'FontSize',num)：y 坐标轴名设为 str，字体大小为 num，默认为 11
  • zlabel(str,'FontSize',num)：z 坐标轴名设为 str，字体大小为 num，默认为 11
1
2
3
4
5
6
7
>> figure
>> [X,Y,Z]=peaks(25);
>> surf(X,Y,Z)
>> title('peak')
>> xlabel('x')
>> ylabel('y')
>> zlabel('z','FontSize',20)

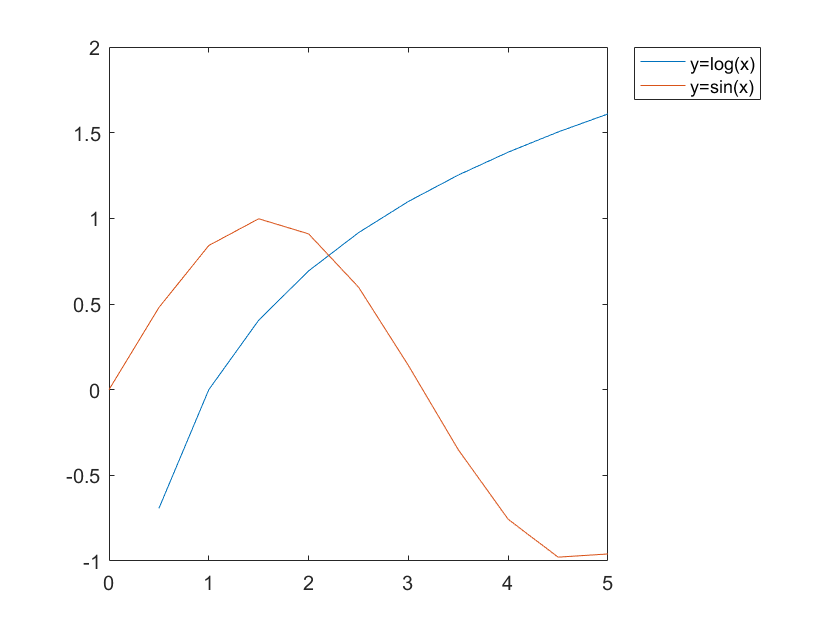
图例

在 matlab 中，生成的图例利用 legend() 函数，其与绘制的图形一一对应，并且默认处于右上角位置

  • legend(str1,str2,...)：依次生成图例 str1、str2、…、strn
  • legend(str1,str2,...,strn,'Location',pos)：依次生成图例 str1、str2、…、strn，并将图例至于 pos 位置
  • legend off：关闭图例

关于 str 的说明：当需要在图例中输出下标、希腊字母等特殊符号时，利用 latex 语法即可

关于 pos 的说明：

参数字符串 含 义 参数字符串 含 义
North 放置在图形的最上端 NorthEast 放置在图形的右上角，默认位置
South 放置在图形的最下端 NorthWest 放置在图形的左上角
East 放置在图形的最右端 SouthEast 放置在图形的右下角
West 放置在图形的最左端 SouthWest 放置在图形的左下角
NorthOutside 放置在图形外的最上端 NorthEastOutside 放置在图形外的右上角
SouthOutsi 放置在图形外的最下端 NorthWestOutside 放置在图形外的左上角
EastOutside 放置在图形外的最右端 SouthEastOutside 放置在图形外的右下角
WestOutside 放置在图形外的最左端 SouthWestOutside 放置在图形外的左下角 
1
2
3
4
5
6
7
8
>> figure
>> hold on
>> x=0:0.5:5;
>> y1=log(x);
>> y2=sin(x);
>> plot(x,y1)
>> plot(x,y2)
>> legend('y=log(x)','y=sin(x)','Location','NorthEastOutside')

【坐标轴】

有时需要对坐标轴范围进行调整，可利用以下函数：

  • xlim([a,b])：查看 x 轴的范围
  • ylim([a,b])：查看 y 轴的范围
  • zlim([a,b])：查看 z 轴的范围
  • set(gca,'xtick',[a:step:b])：调整的 x 轴的刻度范围
  • set(gca,'ytick',[a:step:b])：调整的 y 轴的刻度范围
  • set(gca,'ztick',[a:step:b])：调整的 z 轴的刻度范围
  • axis auto：采取坐标轴默认设置
  • asis on：打开坐标轴标签
  • asis off：关闭坐标轴标签

注：

  1. 在设置刻度时，可以一并将坐标轴的范围改变：set(gca,'xlim',[a,b],'xtick',[a:step:b])
  2. 对于柱状图来说，想改变其 x 轴下标，利用 set(gca,xtick',[a,b,c,...]) 即可
1
2
3
4
5
6
7
8
9
>> figure
>> hold on
>> x=0:0.5:5;
>> y1=log(x);
>> y2=sin(x);
>> plot(x,y1)
>> plot(x,y2)
>> ylim([-1,1.5])
>> set(gca,'xtick',[0:0.5:5])

【其他】

鼠标交互

matlab 中提供了允许鼠标与图形交互的指令：ginput、gtext、zoom

除了 ginput 只能用于二维图形外，其他两个适用于所有图形

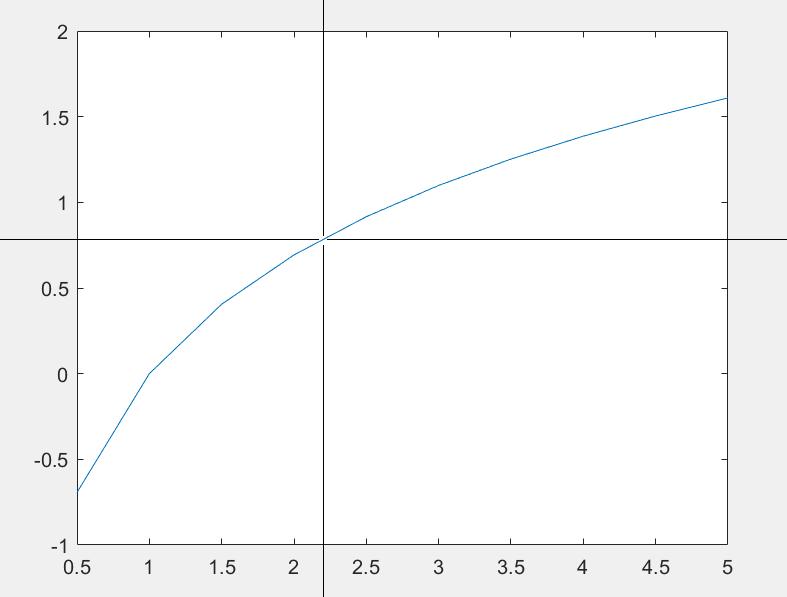
在二维图形中，一般将 ginput 与 zoom 混合使用，以得到较为准确的数据

  • [x,y]=ginput(n)：用鼠标从二维图形中获得 n 个点的数据坐标。在该命令执行后，会将图像调到前台，光标变为十字，通过移动鼠标来定位，通过点击来获取数据，待取完 n 个点后，图形会自动切回后台
运行效果 运行结果
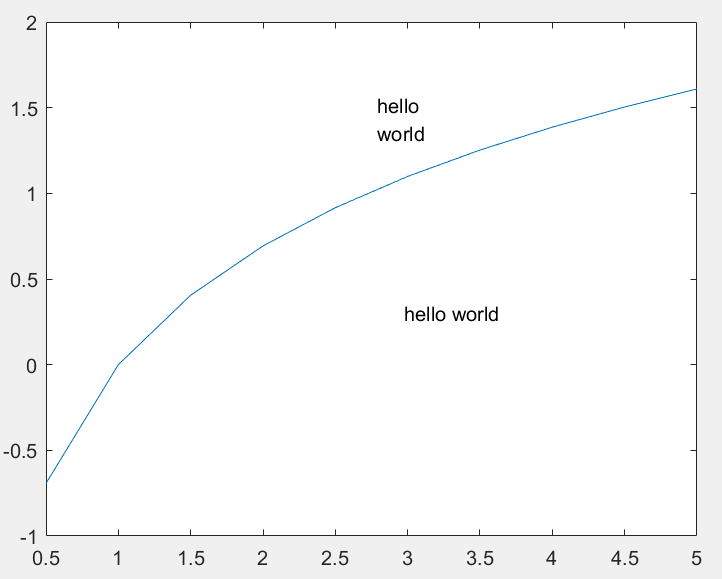
  • gtext(str)：用鼠标将字符串或元胞字符数组放置到图形中，作为文字说明。在该命令执行后，会将图像调到前台，光标变为十字，通过使用鼠标定位，定位到待放置区域后，右击即可完成放置
运行效果 运行结果
  • zoom：用于设定图形缩放
    • zoom xon：规定当前图形的 x 轴可进行缩放
    • zoom yon：规定当前图形的 y 轴可进行缩放
    • zoom on：规定当前图形可进行缩放
    • zoom off：规定当前图形不可进行缩放
    • zoom out：返回图形初始状态

特殊坐标轴

双坐标轴

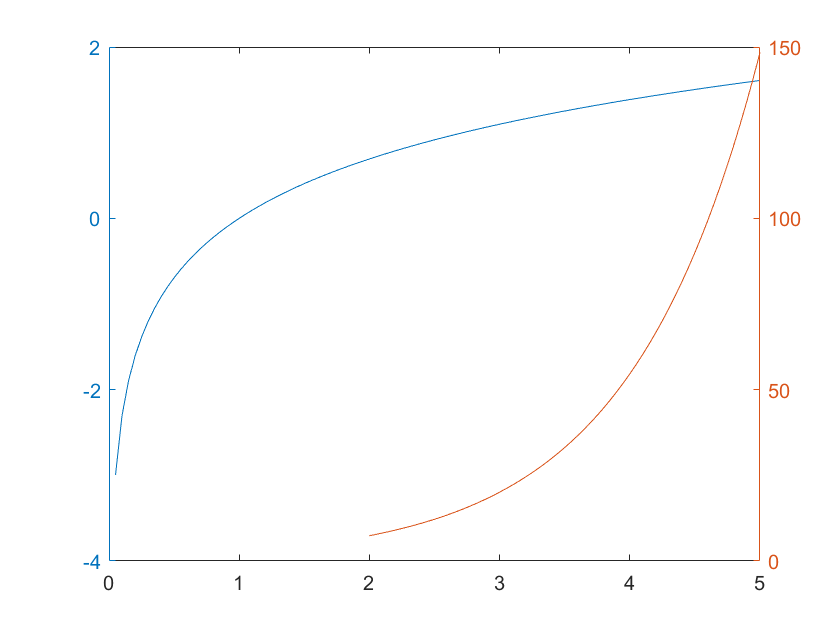
有时需要将同一自变量不同的两个量纲的变化绘制到同一张图上，此时就需要双坐标轴

  • plotyy(X1,Y1,X2,Y2)：以左右不同的纵轴分布绘制 X1-Y1 和 X2-Y2 两条曲线
1
2
3
4
5
6
>> figure
>> x1=0:0.05:5;
>> y1=log(x1);
>> x2=2:0.05:5;
>> y2=exp(x2);
>> plotyy(x1,y1,x2,y2)

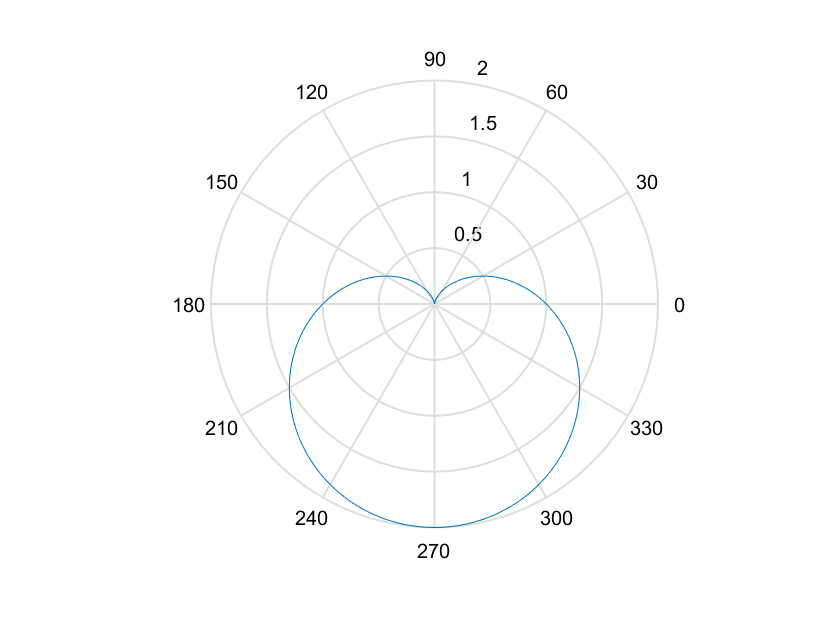
极坐标

利用 polar() 函数可完成极坐标图的绘制

  • polar(theta,rho)：以 theta 为极角，以 rho 为极径绘制极坐标图形
1
2
3
4
>> figure
>> theta=-2*pi:.01:2*pi;
>> rho=(1-sin(theta));
>> polar(theta,rho)

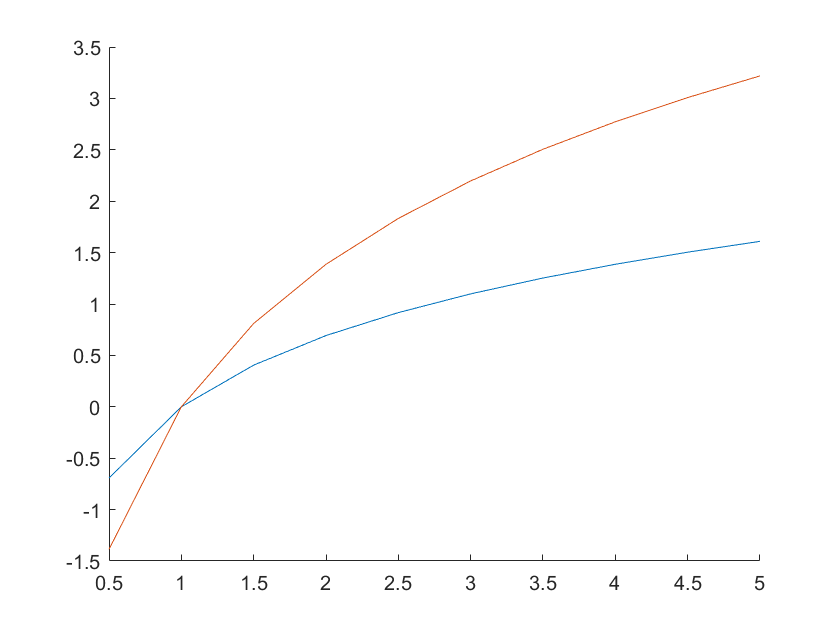
对数坐标

除笛卡尔坐标系、极坐标系外，还有对数坐标系，其可以将处于低次幂的数据清晰显示出来

  • semilogx(X,Y)：以 X 和 Y 在对数坐标系上来绘制图形，x 轴为对数制，y 轴仍为笛卡尔制
  • loglog(X,Y)：以 X 和 Y 在对数坐标系上来绘制图形，x 轴、y 轴均为对数制
1
2
3
4
5
6
7
8
9
>> figure
>> x=0:0.05:5;
>> y=log(x);

>> subplot(1,2,1)
>> semilogx(x,y)

>> subplot(1,2,2)
>> loglog(x,y)

表达式绘制

函数随着自变量的变化趋势是未知的，如果自变量的离散区间不合理，则无法准确地反应函数的变化趋势

plot() 函数自变量的趋势即是我们所给定的，但有时我们给定的离散区间往往不那么合理，此时可以利用 fplot() 函数，其通过自适应算法，来给出离散区间

  • fplot(Fun,[a,b])：在区间 [a,b] 内，绘制函数 Fun 的图形
  • fplot(Fun,[a,b],tol)：在区间 [a,b] 内，绘制函数 Fun 的图形，tol 为相对误差允许范围，默认为 1E6
  • fplot(Fun,[xmin,xmax],[ymin,ymax])：在二维区间 [xmin,xmax]、[ymin,ymax] 内，绘制函数 Fun 的图形
  • fplot(Fun,[xmin,xmax],[ymin,ymax],tol)：在二维区间 [xmin,xmax]、[ymin,ymax] 内，绘制函数 Fun 的图形，tol 为相对误差允许范围，默认为 1E6
1
2
3
4
>> figure
>> f=@(x)sin(x);
>> lim=[-2*pi,2*pi];
>> fplot(f,lim)

感谢您对我的支持，让我继续努力分享有用的技术与知识点！