潜在狄利克雷分配 LDA

【概述】

潜在狄利克雷分配（Latent Dirichlet Allocation，LDA）是文本集合的生成概率模型，其假设话题由单词的多项分布表示，文本由话题的多项分布表示，单词分布和话题分布的先验分布都是狄利克雷分布，文本内容不同是由于它们的话题分布不同

LDA 模型表示了文本集合自动生成过程：首先，基于单词分布的先验分布（狄利克雷分布）生成多个单词分布，即决定多个话题内容；之后，基于话题分布的先验分布（狄利克雷分布）生成多个话题分布，即决定多个文本内容；最后，基于每一个话题分布生成话题序列，针对每一个话题，基于话题的单词分布生成单词，整体构成一个单词序列，即生成文本，重复这个过程生成所有文本

如下图所示，文本的单词序列是观测变量，文本的话题序列是隐变量，文本的话题分布和话题的单词分布也是隐变量

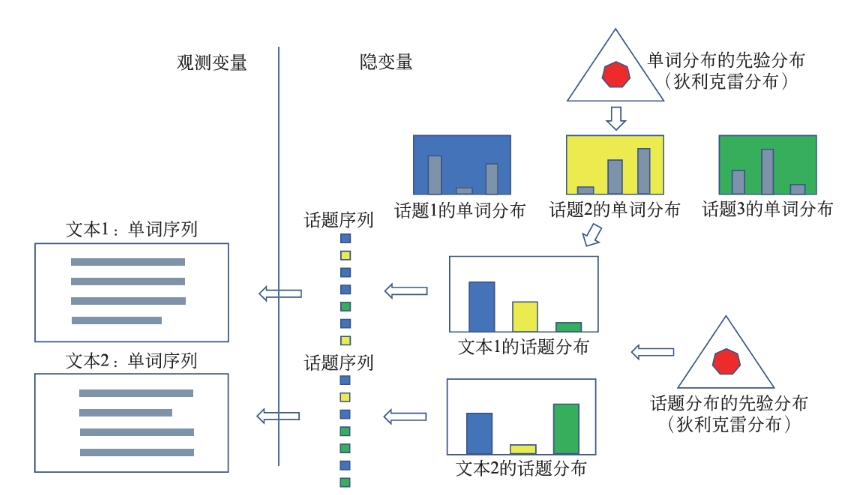
LDA 是概率图模型，其以狄利克雷分布为多项分布的先验分布，学习就是给定文本集合，通过后验概率分布的估计，推断模型的所有参数，利用 LDA 进行话题分析，就是对给定文本集合，学习到每个文本的话题分布，以及每个话题的单词分布

可以认为 LDA 是 PLSA 的扩展，相同点是两者都假设话题是单词的多项分布，文本是话题的多项分布，不同点是 LDA 使用狄利克雷分布作为先验分布，而 PLSA 不使用先验分布，或者说假设先验分布是均匀分布，此外，学习过程 LDA 基于贝叶斯学习，而 PLSA 基于极大似然估计

【模型定义】

模型要素

给定容量为 $V$ 的单词集合 $W=\{w_1,w_2,\cdots,w_V\}$，容量为 $M$ 的文本集合 $D=\{\mathbf{w}_1,\mathbf{w}_2,\cdots,\mathbf{w}_M\}$，容量为 $K$ 的话题集合 $Z=\{z_1,z_2,\cdots,z_K\}$

对于其中的第 $m$ 个文本 $\mathbf{w}_m$，其是一个单词序列，即：

$$\mathbf{w}_m = (w_{m1},w_{m2},\cdots,w_{mn},\cdots,w_{mN_m}),\quad n=1,2,\cdots,N_m$$

其中，$w_{mn}$ 是文本 $\mathbf{w}_m$ 中的第 $n$ 个单词，$N_m$ 是文本 $\mathbf{w}_m$ 中单词的个数

每一个话题 $z_k$ 由一个单词的条件概率分布 $p(w|z_k),w\in W$ 决定，分布 $p(w|z_k)$ 服从多项分布，其参数为 $\boldsymbol{\varphi}_k$，服从狄利克雷分布，超参数为 $\boldsymbol{\beta}$，两者均为 $V$ 维向量

$$\begin{gather*} \boldsymbol{\varphi}_k=(\varphi_{k1},\varphi_{k2},\cdots,\varphi_{kV}) \\ \boldsymbol{\beta}=(\beta_1,\beta_2,\cdots,\beta_V) \\ \end{gather*}$$

其中，$\varphi_{kv}$ 表示话题 $z_k$ 生成单词 $w_v$ 的概率，所有话题的参数向量构成一个 $K\times V$ 维矩阵 $\boldsymbol{\phi} = \{\boldsymbol{\varphi}_k\}^{K}_{k=1}$

每一个文本 $\mathbf{w}_m$ 由一个话题的条件概率分布 $p(z|\mathbf{w}_m),z\in Z$ 决定，分布 $p(z|\mathbf{w}_m)$ 服从多项分布，其参数为 $\boldsymbol{\theta}_m$，服从狄利克雷分布，超参数为 $\boldsymbol{\alpha}$，两者均为 $K$ 为向量

$$\begin{gather*} \boldsymbol{\theta} = (\theta_{m1},\theta_{m2},\cdots,\theta_{mK}) \\ \boldsymbol{\alpha} = (\alpha_{1},\alpha_{2},\cdots,\alpha_{K}) \end{gather*}$$

其中，$\theta_{mk}$ 表示文本 $\mathbf{w}_m$ 生成话题 $z_k$ 的概率，所有文本的参数向量构成一个 $M\times K$ 维矩阵 $\boldsymbol{\Theta} = \{\boldsymbol{\theta}_m\}_{m=1}^M$

综上所述，对于文本 $\mathbf{w}_m$ 中的每一个单词 $w_{mn}$，均由该文本的话题分布 $p(z|\mathbf{w}_m)$ 以及所有话题的单词分布 $p(w|z_k)$ 决定

生成过程

对于给定的单词集合 $W$，文本集合 $D$，话题集合 $Z$，以及狄利克雷分布的超参数向量 $\boldsymbol{\alpha},\boldsymbol{\beta}$

首先，随机生成 $K$ 个话题的单词分布，即按照狄利克雷分布 $\text{Dir}(\boldsymbol{\beta})$ 随机生成一个参数向量 $\boldsymbol{\varphi}_k$，$\boldsymbol{\varphi}_k\sim \text{Dir}(\boldsymbol{\beta})$，作为话题 $z_k$ 的单词分布 $p(w|z_k),w\in W,k=1,2\cdots, K$

然后，随机生成 $M$ 个文本的话题分布，即按照狄利克雷分布 $\text{Dir}(\boldsymbol{\alpha})$ 随机生成一个参数向量 $\boldsymbol{\theta}_m$，$\boldsymbol{\theta}_m\sim \text{Dir}(\boldsymbol{\alpha})$，作为文本 $\mathbf{w}_m$ 的话题分布 $p(z|\mathbf{w}_m),z\in Z,m=1,2\cdots, M$

最后，随机生成 $M$ 个文本的 $N_m$ 个单词，对于文本 $\mathbf{w}_m$ 的单词 $w_{mn}$，其生成过程如下：

1. 按照多项分布 $\text{Mult}(\boldsymbol{\theta}_m)$ 随机生成一个话题 $z_{mn}$，$z_{mn}\sim \text{Mult}(\boldsymbol{\theta}_m)$
2. 按照多项分布 $\text{Mult}(\boldsymbol{\varphi}_{z_{mn}})$ 随机生成一个单词 $w_{mn}$，$w_{mn}\sim\text{Mult}(\boldsymbol{\varphi}_{z_{mn}})$

文本 $\mathbf{w}_{m}$ 本身是单词序列 $\mathbf{w}_m=(w_{m1},w_{m2},\cdots,w_{mN_m})$，对应着隐式的话题序列 $\mathbf{z}_m=(z_{m1},z_{m2},\cdots,z_{mN_m})$

在 LDA 的文本生成过程中，假定话题个数 $K$ 给定，但实际通常通过实验选定，狄利克雷分布的超参数向量 $\boldsymbol{\alpha}$ 和 $\boldsymbol{\beta}$ 也是事先给定的，在没有其他先验知识的情况下，通常假设向量 $\boldsymbol{\alpha}$ 和 $\boldsymbol{\beta}$ 的所有分量均为 $1$，此时文本的话题分布 $\boldsymbol{\theta}_m$ 是对称的，话题的单词分布 $\boldsymbol{\varphi}_k$ 也是对称的

【概率图模型】

LDA 模型本质上是一种概率图模型，通常使用板块图来表示，图中各结点均为随机变量，其中实心结点表示观测变量，空心结点表示隐变量，有向边表示概率依存关系，矩形表示重复，矩形内的数字表示重复的次数

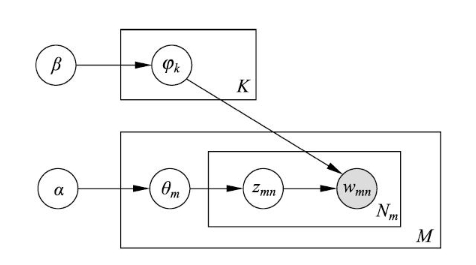
如上图所示，其含义如下

• 结点 $\boldsymbol{\alpha}$ 和 $\boldsymbol{\beta}$ 是模型的超参数，结点 $\boldsymbol{\varphi}_k$ 表示话题的单词分布的参数，结点 $\boldsymbol{\theta}_m$ 表示文本的话题分布的参数，结点 $z_{mn}$ 表示话题，结点 $w_{mn}$ 表示单词
• 结点 $\boldsymbol{\beta}$ 指向结点 $\boldsymbol{\varphi}_k$，重复 $K$ 次，表示根据超参数 $\boldsymbol{\beta}$ 生成 $K$ 个话题的单词分布的参数 $\boldsymbol{\varphi}_k$
• 结点 $\boldsymbol{\alpha}$ 指向结点 $\boldsymbol{\theta}_m$，重复 $M$ 次，表示根据超参数 $\boldsymbol{\alpha}$ 生成 $M$ 个文本的话题分布的参数 $\boldsymbol{\theta}_m$
• 结点 $\boldsymbol{\theta}_m$ 指向结点 $z_{mn}$，重复 $N_m$ 次，表示根据文本的话题分布 $\boldsymbol{\theta}_m$ 生成 $N_m$ 个话题 $z_{mn}$
• 结点 $z_{mn}$ 指向结点 $w_{mn}$，同时 $K$ 个结点 $\boldsymbol{\varphi}_k$ 也指向结点 $w_{mn}$，表示根据话题 $z_{mn}$ 以及 $K$ 个话题的单词分布 $\boldsymbol{\varphi}_k$ 生成单词 $w_{mn}$

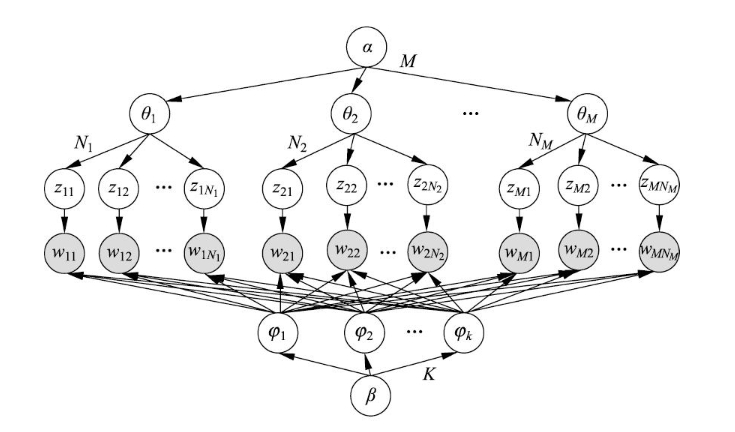
将板块表示展开后，就成为了普通的有向图表示，图中各结点均为随机变量，其中实心结点表示观测变量，空心结点表示隐变量，有向边表示概率依存关系

如下图所示，可以看出 LDA 是相同随机变量被重复多次使用的概率图模型

【可交换性】

若随机变量的联合概率分布对随机变量的排列不变，则称该随机变量序列是可交换的（Exchangeable）

$$P(x_1,x_2,\cdots,x_N) = P(x_{\pi(1)},x_{\pi(2)},\cdots,x_{\pi(N)})$$

其中，$\pi(1),\pi(2),\cdots,\pi(N)$ 代表自然数 $1,2,\cdots,N$ 的任意一个排列

一个无限的随机变量序列是无限可交换的（Infinitely Exchangeable），即它的任意一个有限子序列都是可交换的，因此，对于一个随机变量序列 $X_1,X_2,\cdots,X_N,\cdots$，若其是独立同分布的，那么它们是无限可交换的

随机变量序列可交换的假设在贝叶斯学习中经常使用，根据 De Finetti 定理，任意一个无限可交换的随机变量序列对一个随机参数是条件独立同分布的，即任意一个无限可交换的随机变量序列 $X_1,X_2,\cdots, X_i,\cdots$ 的基于一个随机参数 $Y$ 的条件概率，等于基于这个随机参数 $Y$ 的各个随机变量 $X_1,X_2,\cdots, X_i,\cdots$ 的条件概率的乘积

$$P(X_1,X_2,\cdots, X_i,\cdots|Y)=P(X_1|Y)P(X_2|Y)\cdots P(X_i|Y)\cdots$$

LDA 假设文本由无限可交换的话题序列组成，根据 De Finetti 定理可知，其实际上是假设文本中的话题对一个随机参数是条件独立同分布的，因此在参数给定的条件下，文本中的话题的顺序可以忽略

【生成概率】

LDA 模型整体是由观测变量和隐变量组成的联合概率分布，可以表示为：

$$p(\mathbf{w},\mathbf{z},\boldsymbol{\Theta},\boldsymbol{\phi}|\boldsymbol{\alpha},\boldsymbol{\beta}) = \prod_{k-1}^K p(\boldsymbol{\varphi}_k|\boldsymbol{\beta})\prod_{m=1}^M p(\boldsymbol{\theta}_m|\boldsymbol{\alpha})\prod_{n=1}^{N_m} p(z_{mn}|\boldsymbol{\theta}_m)p(w_{mn}|z_{mn},\boldsymbol{\phi})$$

其中，观测变量 $\mathbf{w}$ 表示所有文本中的单词序列，隐变量 $\mathbf{z}$ 表示所有文本中的话题序列，隐变量 $\boldsymbol{\Theta}$ 表示所有文本的话题分布的参数，隐变量 $\boldsymbol{\phi}$ 表示所有话题的单词分布的参数，$\boldsymbol{\alpha},\boldsymbol{\beta}$ 是超参数，$p(\boldsymbol{\varphi}_k|\boldsymbol{\beta})$ 表示超参数 $\boldsymbol{\beta}$ 给定条件下第 $k$ 个话题的单词分布的参数 $\boldsymbol{\varphi}_k$ 的生成概率，$p(\boldsymbol{\theta}_m|\boldsymbol{\alpha})$ 表示超参数 $\boldsymbol{\alpha}$ 给定条件下第 $m$ 个文本的话题分布的参数 $\boldsymbol{\theta}_m$ 的生成概率，$p(z_{mn}|\boldsymbol{\theta}_m)$ 表示第 $m$ 个文本的话题分布 $\boldsymbol{\theta}_m$ 给定条件下文本的第 $n$ 个位置的话题 $z_{mn}$ 的生成概率，$p(w_{mn}|z_{mn},\boldsymbol{\phi})$ 表示在第 $m$ 个文本的第 $n$ 个位置的话题 $z_{mn}$ 以及所有话题的分布的参数 $\boldsymbol{\phi}$ 给定条件下第 $m$ 个文本的第 $n$ 个位置的单词 $w_{mn}$ 的生成概率

第 $m$ 个文本的联合分布概率可以表示为：

$$p(\mathbf{w}_m,\mathbf{z}_m,\boldsymbol{\theta}_m,\boldsymbol{\phi}|\boldsymbol{\alpha},\boldsymbol{\beta}) = \prod_{k=1}^K p(\boldsymbol{\varphi}_k|\boldsymbol{\beta}) p(\boldsymbol{\theta}_m|\alpha) \prod_{n=1}^{N_m} p(z_{mn}|\boldsymbol{\theta}_m) p(w_{mn}|z_{mn},\boldsymbol{\phi})$$

其中，$\mathbf{w}_m$ 表示该文本中的单词序列，$\mathbf{z}_m$ 表示该文本的话题序列，$\boldsymbol{\theta}_m$ 表示该文本的话题分布参数

LDA 模型的联合分布含有隐变量，对隐变量进行积分，可得到边缘分布

参数 $\boldsymbol{\theta}_m$ 和 $\boldsymbol{\phi}$ 给定条件下第 $m$ 个文本的生成概率是：

$$p(\mathbf{w}_m|\boldsymbol{\theta}_m,\boldsymbol{\phi}) = \prod_{n=1}^{N_m} \Big[ \sum_{k=1}^K p(z_{mn}=k|\boldsymbol{\theta}_m)p(w_{mn}|\boldsymbol{\varphi}_k) \Big]$$

超参数 $\boldsymbol{\alpha},\boldsymbol{\beta}$ 给定条件下第 $m$ 个文本的生成概率是：

$$p(\mathbf{w}_m|\boldsymbol{\alpha},\boldsymbol{\beta}) = \prod_{k=1}^K \int p(\boldsymbol{\varphi}_k|\boldsymbol{\beta}) \Bigg[\int p(\boldsymbol{\theta}_m|\boldsymbol{\alpha}) \prod_{n=1}^{N_m} \Big[ \sum_{l=1}^K p(z_{mn=l}|\boldsymbol{\theta}_m) p(w_{mn}|\boldsymbol{\varphi}_l) \Big] d\boldsymbol{\theta}_m \Bigg] d\boldsymbol{\varphi}_k$$

超参数 $\boldsymbol{\alpha},\boldsymbol{\beta}$ 给定条件下所有文本的生成概率是：

$$p(\mathbf{w}|\boldsymbol{\alpha},\boldsymbol{\beta}) = \prod_{k=1}^K \int p(\boldsymbol{\varphi}_k|\boldsymbol{\beta}) \Bigg[ \prod_{m=1}^M \int p(\boldsymbol{\theta}_m|\boldsymbol{\alpha}) \prod_{n=1}^{N_m} \Big[ \sum_{l=1}^K p(z_{mn}=l|\boldsymbol{\theta}_m)p(w_{mn}|\boldsymbol{\varphi}_l) \Big] d\boldsymbol{\theta}_m \Bigg] d\boldsymbol{\varphi}_k$$