K-Means

【概述】

K-均值（K-Means）是最基础最常用的聚类算法，其是基于样本集合划分的聚类算法，属于原型聚类，同时，由于每个数据点都被精确地分配到一个簇中，因此其也是硬聚类算法的一种

K-Means 的基本思想是：将样本集合划分为 $K$ 个子集，构成 $K$ 个簇，通过迭代来寻找一种划分，使得每个样本到其所属簇的中心距离最小

K-Means 容易理解，聚类效果较好，在处理大数据集时，可保证较好的伸缩性，算法复杂度较低，但 K 值需要人为确定，不同的 K 值得到的结果不同，同时，其对初始的簇心敏感，不同选取方式会得到不同结果，不适合太离散、样本类别不平衡、非凸形状的分类

【模型】

对于给定容量为 $n$ 的样本集 $D=\{\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\}$，第 $i$ 个样本的输入 $\mathbf{x}_i$ 具有 $m$ 个特征值，即：$\mathbf{x}_i = (x_i^{(1)},x_i^{(2)},\cdots,x_i^{(m)})\in \mathbb{R}^{m}$

K-Means 的目标是将 $n$ 个样本划分到 $K$ 个不同的簇 $\mathcal{C}=\{C_1,C_2,\cdots,C_K\}$ 中，以形成对样本集 $D$ 的划分，其中，对于簇 $C_i$ 和 $C_j$，有：

$$\begin{gather*} C_i \cap C_j = \varnothing \\ \bigcup_{k=1}^K C_k = D \end{gather*}$$

聚类是一个多对一函数，若将每个样本用一个整数 $i\in\{1,2,\cdots,n\}$，每个簇也用一个整数 $\mathcal{C}\in\{1,2,\cdots,K\}$ 来表示，那么聚类可以用函数 $\mathcal{C}=C(i)$ 来表示

综上所述，K-Means 聚类的模型实质上是一个从样本到类的函数

【策略】

K-Means 可归结为样本集合 $D$ 的划分，或者从样本到簇的函数的选择问题，其策略是通过损失函数的最小化来选取最优的划分或函数 $C^{*}(\cdot)$

通常来说，在 K-Means 中会采用欧式距离来作为样本间的距离 $d(\mathbf{x}_i,\mathbf{x}_j) $，即：

$$\begin{align*} d(\mathbf{x}_i,\mathbf{x}_j) &= ||\mathbf{x}_i-\mathbf{x}_j||^2 \\ &= \sum_{l=1}^{m} (x_{i}^{(l)}-x_{j}^{(l)})^2 \end{align*}$$

在距离 $d(\mathbf{x}_i,\mathbf{x}_j) $ 的基础上，定义样本与其所属簇的簇心的距离的总和为损失函数，即：

$$\begin{align*} E(C) &= \sum_{k=1}^K \sum_{\mathcal{C}(i)=k} d(\mathbf{x}_i,\overline{\mathbf{x}}_k) \\ &= \sum_{k=1}^K \sum_{\mathcal{C}(i)=k} ||\mathbf{x}_i-\overline{\mathbf{x}}_k|| ^2 \end{align*}$$

其中，$\overline{\mathbf{x}}_k=(x_{k}^{(1)},x_{k}^{(2)},\cdots,x_{k}^{(m)})$ 是第 $k$ 个簇的簇心

$E(C)$ 也被称为能量，实质上表示了相同簇中的样本的相似程度，K-Means 就是求解 $E(C) $ 的最优化问题

$$\begin{align*} C^{*} &= \arg \min_C E(C) \\ &= \arg \min_C \sum_{k=1}^K \sum_{\mathcal{C}(i)=k} ||\mathbf{x}_i-\overline{\mathbf{x}}_k|| ^2 \end{align*}$$

当相似样本被聚到同簇时，损失函数值最小，这个目标函数的最优化能达到聚类的目的，但是这是一个组合优化问题，$n$ 个样本分到 $K$ 簇，所有可能分法的数目是：

$$S(n,K) = \frac{1}{K!} \sum_{k=1}^{K} (-1)^{K-k} \left(\begin{array}{c}K\\k\end{array}\right)$$

这个数字是指数级的，实际上，K-Means 的最优解求解问题是 NP 难问题，现实中常采用迭代法求解

【算法】

基本思想

K-Means 的算法是一个迭代的过程，每次迭代包括两个步骤：

1. 选择 $k$ 个簇的簇心，将样本逐个指派到与其最近的中心的簇中，得到一个聚类结果
2. 更新每个簇的样本均值，作为簇的新的簇心

重复以上步骤，直到收敛为止

具体步骤如下：

Step1：对于给定的簇心 $(\mathbf{m}_1,\mathbf{m}_2,\cdots,\mathbf{m}_K)$，求一个划分 $C$，使得目标函数极小化：

$$\min_{C} \sum_{k=1}^K \sum_{C(i)=k} ||\mathbf{x}_i-\mathbf{m}_k||^2$$

即在簇心确定的情况下，将每一样本 $\mathbf{x}_i$ 分到每一个簇中，使样本和其所属簇心间的距离总和最小

求解结果后，将每一样本 $\mathbf{x}_i$ 指派到与其最近的簇心 $\mathbf{m}_k$ 的簇 $C_{k}$

Step2：对于给定的划分 $C$，再求各簇的簇心 $(\mathbf{m}_1,\mathbf{m}_2,\cdots,\mathbf{m}_K)$，使得目标函数极小化：

$$\min_{\mathbf{m}_1,\mathbf{m}_2,\cdots,\mathbf{m}_K} \sum_{k=1}^K \sum_{C(i)=k} ||\mathbf{x}_i-\mathbf{m}_k||^2$$

即在划分确定的情况下，使样本和其所属的簇的簇心间的距离总和最小

求解结果后，对于每个包含 $n_k$ 个样本的簇 $C_k$，更新其均值 $\mathbf{m}_k$：

$$\begin{gather*} \mathbf{m}_k = \frac{1}{n_k} \sum_{C(i)=k} \mathbf{x}_i, \quad k=1,2,\cdots,K \\ n_k = \sum_{i=1}^n \mathbb{I}(C(i)=k) \end{gather*}$$

重复以上两个步骤，直到划分不再改变，得到聚类结果

算法流程

输入：$n$ 个样本的集合 $D$

输出：样本集合的聚类 $C^{*}$

算法流程：

Step1：初始化。令 $t=0$，随机选择 $K$ 个样本点作为初始聚类中心

$$\mathbf{m}^{(0)} = (m_1^{(0)},m_2^{(0)},\cdots,m_K^{(0)})$$

Step2：对样本进行聚类。对于固定的簇心 $\mathbf{m}^{(t)} = (m_1^{(t)},m_2^{(t)},\cdots,m_K^{(t)})$，计算每个样本 $\mathbf{x}_i$ 到簇心的距离，将每个样本指派到与其最近的簇心的簇中，构成聚类结果 $C^{(t)}$

Step3：计算新的簇心。对于聚类结果 $C^{(t)}$，计算当前各个类中的样本的均值，作为新的簇心

$$\mathbf{m}^{(t+1)} = (m_1^{(t+1)},m_2^{(t+1)},\cdots,m_K^{(t+1)})$$

Step4：若迭代收敛，或符合停止条件，输出 $C^{*}=C^{t}$，否则，令 $t=t+1$，返回 Step2

【手肘法】

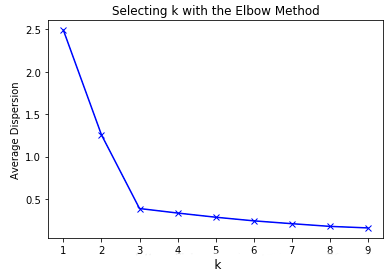
K 值的选择一般基于实验和多次实验结果，最简单的方法是手肘法，即通过尝试不同的 K 值并将对应的损失函数画成折线，然后选取折线的拐点作为最佳 K 值

如下图所示，手肘法认为图中的拐点 $k=3$ 为最佳 K 值

【sklearn 实现】

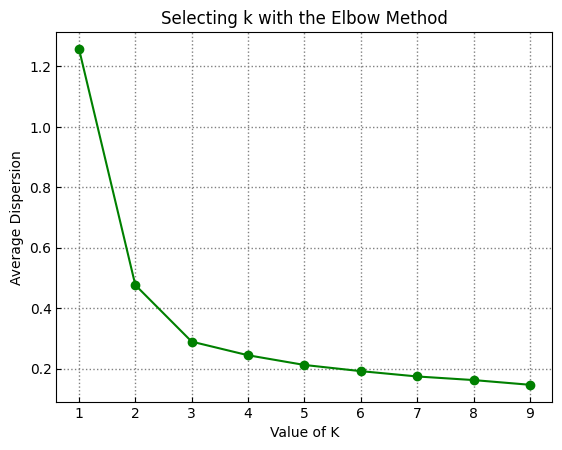
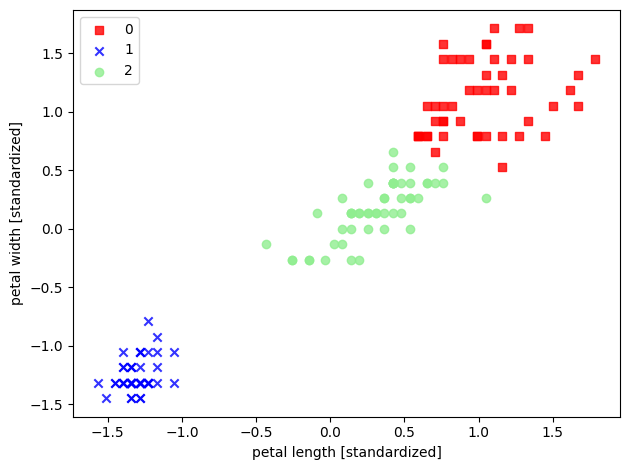
以 sklearn 中的鸢尾花数据集为例，选取其后两个特征来实现 K-Means

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
from matplotlib.colors import ListedColormap

# 特征提取
def deal_data():
    iris = load_iris()  # sklearn的鸢尾花数据集
    # iris分为三类，前50行一类，51-100行一类，101-150行一类
    X = iris.data[:, [2, 3]] # 选用后两个特征作为样本特征
    return X

# 数据标准化
def standard_scaler(X):
    sc = StandardScaler() # 初始化一个sc对象去对数据集作变换
    scaler = sc.fit(X) # 归一化，存有计算出的均值和方差
    X_std = scaler.transform(X) # 利用 scaler 进行标准化
    return X_std

# 模型训练
def train_model(features, k):
    # 建立聚类器
    model = KMeans(n_clusters=k)
    # 聚类
    model.fit(features)
    return model

# 手肘法获取最佳K值
def get_k(X):
    mean_distortions = []
    for k in range(1, 10):
        model = train_model(X, k)
        mean_distortions.append(sum(np.min(cdist(X, model.cluster_centers_, 'euclidean'), axis=1))/X.shape[0])
        
    # 绘制k-平均距离折线图
    plt.figure()
    plt.tick_params(direction='in')
    plt.grid(color='grey', linestyle=':', linewidth=1)
    plt.plot(range(1, 10), mean_distortions, color='green', marker='o')
    plt.xlabel('Value of K')
    plt.ylabel('Average Dispersion')
    plt.title('Selecting k with the Elbow Method')
    plt.show()

# 可视化
def visualization(X, y):
    # 创建 color map
    markers = ('s', 'x', 'o', '^', 'v')
    colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
    cmap = ListedColormap(colors[:len(np.unique(y))])

     # 全数据集，不同类别样本点的特征作为坐标(x,y)，用不同颜色画散点图
    for idx, cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1], alpha=0.8, c=cmap(idx), marker=markers[idx], label=cl) 
        
    plt.xlabel('petal length [standardized]')
    plt.ylabel('petal width [standardized]')
    plt.legend(loc='upper left')
    plt.tight_layout()
    plt.show()


if __name__ == "__main__":
    # 数据处理
    X = deal_data()

    # 数据标准化
    X_std = standard_scaler(X)

    # 手肘法获取最佳K值
    get_k(X_std)
    k = 3
    
    # 模型训练
    model = train_model(X_std, k)

    # 获取聚类标签
    label_pred = model.labels_ 
    
    # 可视化
    visualization(X_std, label_pred)