【无监督学习】
无监督学习(Unsupervised Learning)是直接从自然数据(无标注数据)中学习预测模型,其没有给定标记过的训练范例,即事先不知道输入数据对应的输出结果是什么,其本质是学习数据中的统计规律、潜在结构
无监督学习所用的数据没有属性或标签这一概念,对于每一个输入实例,给定的输出是对输入的结果分析,可由输入的类别、转换、概率来表示,相应地,可以实现数据的聚类、降维、密度估计
【基本概念】
输入与输出空间
在无监督学习中,输入、输出变量/向量用大写字母表示,习惯上输入变量/向量写为 $X$,输出变量/向量写为 $Z$;输入、输出变量的取值用小写字母表示,习惯上输入变量的取值写为 $x$,输出变量的取值写为 $z$;输入、输出向量的取值用加粗的小写字母表示,习惯上输入向量的取值写为 $\mathbf{x}$,输出向量的取值写为 $\mathbf{z}$
输入与输出的所有可能取值的集合分别称为输入空间、输出空间,分别用 $\mathcal{X}$、$\mathcal{Z}$ 表示,他们可以是有限元素的集合,也可以是整个欧式空间 $\mathbb{R}^n$,即现实空间规则的抽象与推广(从 $n\leq 3$ 到有限 $n$ 维空间)
假设空间
在无监督学习中,包含所有可能的模型的集合称为假设空间
无监督学习的目标是从假设空间中选出给定评价标准下的最优模型
样本
无监督学习通常使用大量的无标注数据进行训练,每个样本是一个实例
对于样本容量为 $N$ 的训练集,表示为:
【模型形式】
针对具体的学习方法,无监督学习可以是概率模型也可以是非概率模型,分别由条件概率分布 $P_{\boldsymbol{\theta}}(Z|X)$、$P_{\boldsymbol{\theta}}(X|Z)$ 或决策函数 $Z=g(X;\boldsymbol{\theta})$ 来表示
对于具体的输入来说,分析时使用学习得到的具体模型写作:$\hat{P}_{\boldsymbol{\theta}}(\mathbf{z}|\mathbf{x})$、$\hat{P}_{\boldsymbol{\theta}}(\mathbf{x}|\mathbf{z})$ 或 $\mathbf{z}=\hat{g}(\mathbf{x};\boldsymbol{\theta})$
其中,$\mathbf{x}\in X$ 是输入,表示样本,$\mathbf{z}\in Z$ 是输出,表示对样本的分析结果,$\theta$ 是参数
【预测任务】
基本思路
无监督学习的基本思想是对给定数据进行某种压缩,从而找到数据的潜在结构
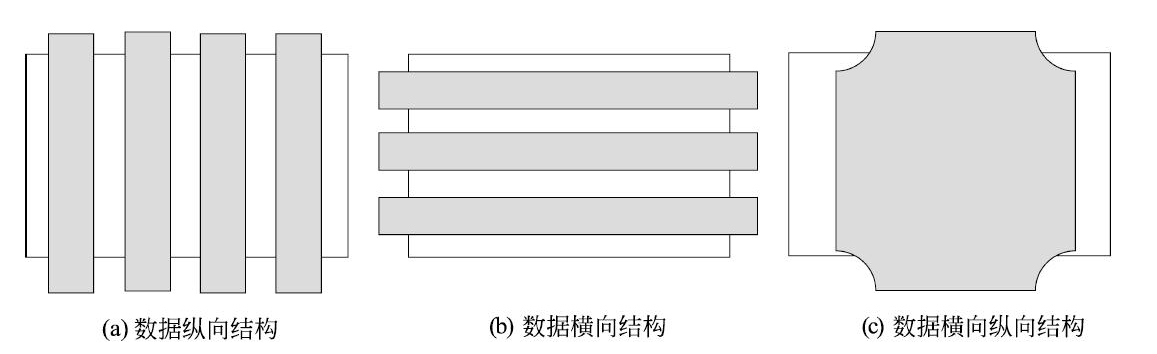
可以考虑发掘数据的纵向结构,把相似的样本聚到同类,即对数据进行聚类。还可以考虑发掘数据的横向结构,把高维空间的向量转换为低维空间的向量,即对数据进行降维。也可以同时考虑发掘数据的纵向与横向结构,假设数据由含有隐式结构的概率模型生成得到,从数据中学习该概率模型
聚类问题
聚类(Clustering),是发现数据集 $X$ 中的纵向结构,即将数据按照相似度聚类成不同的分组,聚类时,样本通常是欧氏空间中的向量,类别是从数据中自动发现的,但类别的个数通常事先给定
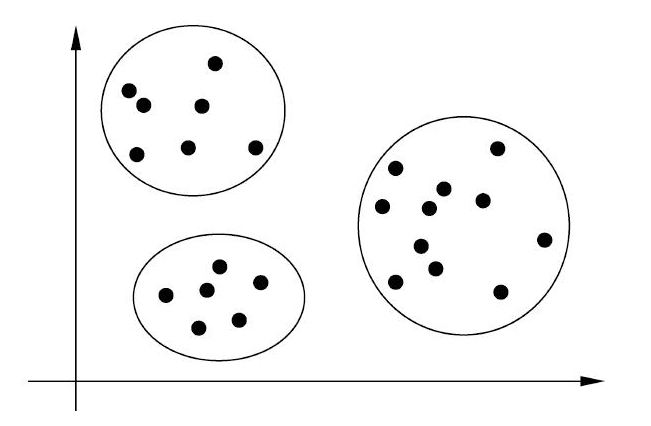
假设输入空间 $X$,输出空间为类别集合 $Z=\{1,2,…,k\}$,对于输入空间 $X$ 中的某一输入 $\mathbf{x_{N+1}}$,由模型 $\hat{P}_{\boldsymbol{\theta}}(Z|X)$ 或 $Z=\hat{g}(X;\boldsymbol{\theta})$ 给出相应的输出 $\mathbf{z_{N+1}}$
当一个样本只能属于一个类时,称为硬聚类(Hard Clustering),此时聚类模型采用函数 $Z=\hat{g}(X;\boldsymbol{\theta})$,当一个样本可以属于多个类时,称为软聚类(Soft Clustering),此时模型采用条件概率分布 $\hat{P}_{\boldsymbol{\theta}}(Z|X)$
降维问题
降维(Dimensionality Reduction),是发现数据集 $X$ 中的横向结构,即将训练数据中的样本从高维空间转到低维空间,以避免数据可能会出现的维度灾难问题,其本质上是在保留数据结构和有用性的同时对数据进行压缩
高维空间通常是高维的欧氏空间,而低维空间是低维的欧氏空间或者流形(Manifold),低维空间不是事先给定,而是从数据中自动发现,但其维数通常是事先给定的
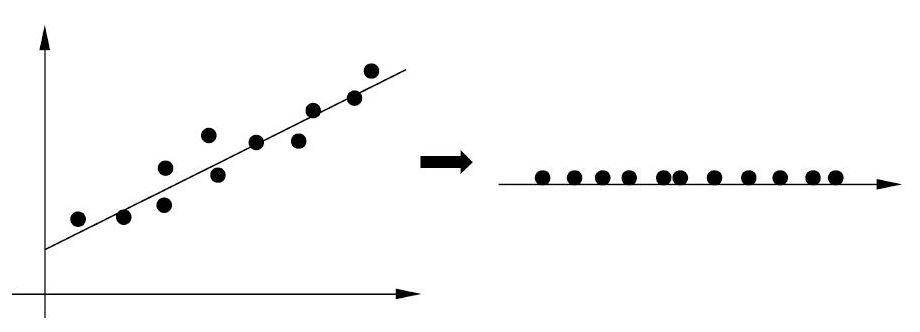
假设输入空间 $X$,输出空间为 $Z$,$\mathbf{x}\in X$ 是样本的高维向量,$\mathbf{z}\in Z$ 是样本的低维向量,对于给定的输入 $\mathbf{x_{N+1}}$,由模型 $Z=\hat{g}(X;\boldsymbol{\theta})$ 给出相应的输出 $\mathbf{z_{N+1}}$,其中 $g$ 可是线性函数,也可是非线性函数
概率模型估计
概率模型估计(Probability Model Estimation)简称概率估计,是指对于给出的无标注数据,寻找分布规律并估计服从这种分布的正确性概率是多少
简单来说,事先给定概率模型的结构类型,或给定概率模型的集合,通过训练数据学习模型的具体结构和参数,学习的目标是找到最有可能生成数据的结构和参数

通常由条件分布 $P_{\Theta}(X|Z)$ 来表示概率估计,对于输入数据 $x\in X$,其可以是连续变量,也可以是离散变量;对于输出数据 $z\in Z$,当模型为隐式结构时,$z$ 为离散变量,当模型为混合模型时,$z$ 表示成分的个数,当模型为概率图模型时,$z$ 表示图的结构
根据贝叶斯公式,软聚类也可看作概率估计问题,即:
其中,$P(Z)$ 为先验概率,且服从均匀分布,因此只需计算出条件概率 $P_{\boldsymbol{\theta}}(X|Z)$ 即可进行软聚类

