【概述】
对于隐马尔可夫模型的概率计算问题,即:给定隐马尔可夫模型 $\lambda=(A,B,\pi)$ 和观测序列 $O=(o_1,o_2,\cdots,o_T)$,计算在模型 $\lambda$ 下观测序列 $O$ 出现的概率 $P(O|\lambda)$
有以下两种概率计算方法:
- 直接计算法:暴力算法,时间复杂度 $O(N^2T)$
- 前向后向法(Forward-Backward Algorithm):前向计算法与后向计算法的统称,本质上是动态规划算法,时间复杂度 $O(N^2T)$
【直接计算法】
直接计算法即按概率公式直接计算,其基本思路是:列举所有可能的长度为 $T$ 的状态序列 $I$,求各状态序列 $I$ 与观测序列 $O$ 联合概率 $P(O,I|\lambda)$,然后对所有可能的状态序列求和,得到 $P(O|\lambda)$
状态序列 $I=(i_1,i_2,\cdots,i_T)$ 的概率为:
对固定的状态序列 $I=(i_1,i_2,\cdots,i_T)$,观测序列 $O=(o_1,o_2,\cdots,o_T)$ 的概率为:
观测序列 $O$ 与状态序列 $I$ 同时出现的联合概率为:
然后,对所有可能的状态序列 $I$ 求和,得到观测序列 $O$ 的概率 $P(O|\lambda)$,即:
但是,直接利用上述公式进行计算的计算量很大,是 $O(TN^T)$ 阶的,随着 $T$ 的增长时间复杂度会呈爆炸式增长,故而该方法在计算上不可行
【前向计算法】
前向概率
对于给定的隐马尔可夫模型 $\lambda=(A,B,\lambda)$,定义到时刻 $t$ 的部分观测序列为 $o_1,o_2,\cdots,o_t$ 且状态为 $q_i$ 的概率为前向概率,记作:
前向概率的递推公式
对于到时刻 $t$ 观测到 $o_1,o_2,\cdots,o_t$ 并在时刻 $t$ 处于状态 $q_j$ 的前向概率 $\alpha_t(j)$,那么结合转移概率 $a_{ji}$,可求得到时刻 $t$ 观测到 $o_1,o_2,\cdots,o_t$ 并在时刻 $t$ 处于状态 $q_j$ 而在 $t+1$ 时刻到达状态 $q_i$ 的联合概率,即:
对在 $t$ 时刻所有可能的 $N$ 个状态 $q_j$ 求和,可得到到时刻 $t$ 观测到 $o_1,o_2,\cdots,o_t$ 并在 $t+1$ 时刻处于状态 $q_i$ 的联合概率,即:

那么,将这个联合概率与观测概率 $b_i(o_{t+1})$ 相乘,即可得到到时刻 $t+1$ 观测到 $o_1,o_2,\cdots,o_t,o_{t+1}$ 并在时刻 $t+1$ 处于状态 $q_i$ 的前向概率 $\alpha_{t+1}(i)$,即:
上式即前向概率的递推公式
观测序列概率的计算
由于到时刻 $T$ 的观测序列为 $o_1,o_2,\cdots,o_T$ 且状态为 $q_i$ 的前向概率为:
故在模型 $\lambda$ 下观测序列 $O$ 出现的概率 $P(O|\lambda)$ 为:
算法流程
综上所述,给出观测序列概率的前向计算法的算法流程
输入:隐马尔可夫模型 $\lambda=(A,B,\pi)$,观测序列 $O=(o_1,o_2,\cdots,o_T)$
输出:观测序列概率 $P(O|\lambda)$
算法步骤如下:
Step 1:算法初始化,对初始时刻 $t=1$,根据初始概率分布 $\pi$ 与观测概率 $b_i(o_1)$,求得初始时刻的状态 $i_1=q_i$ 和观测 $o_1$ 的联合概率,即初始前向概率:
Step 2:根据前向概率的递推公式进行递推
对 $t=1,2,\cdots,T-1$,有:
Step 3:计算在模型 $\lambda$ 下观测序列 $O$ 出现的概率
如下图所示,前向计算法实际是基于状态序列的路径结构,递推计算 $P(O|\lambda)$
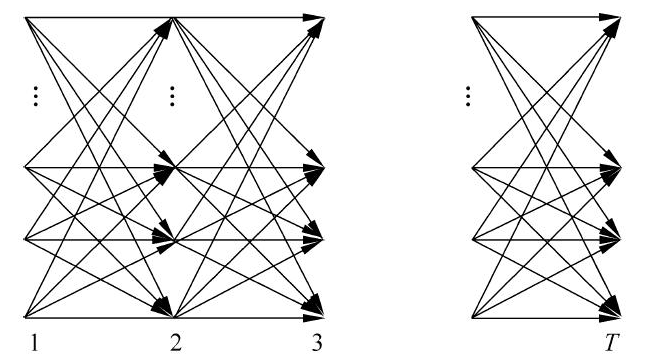
其高效之处在于局部计算前向概率,然后利用路径结构将前向概率递推到全局,进而得到 $P(O|\lambda)$
具体来说,在初始时刻 $t=1$,计算 $\alpha_1(i)$ 的 $N$ 个值($i=1,2,\cdots,N$),在各时刻 $t=1,2,\cdots,T-1$,计算 $\alpha_{t+1}(i)$ 的 $N$ 个值($i=1,2,\cdots,N$),并且每个 $\alpha_{t+1}(i)$ 的计算利用前一时刻 $N$ 个 $\alpha_t(j)$,减小计算量的原因就在于每一次计算都引用了之前的结果,避免了重复计算
这样,利用前向概率计算 $P(O|\lambda)$ 的计算量是 $O(N^2T)$ 阶的
【后向计算法】
后向概率
对于给定的隐马尔可夫模型 $\lambda=(A,B,\lambda)$,定义在 $t$ 时刻状态为 $q_i$ 的条件下,从 $t+1$ 到 $T$ 的部分观测序列为 $o_{t+1},o_{t+2},\cdots,o_T$ 的概率为后向概率,记作:
后向概率的递推公式
为计算在 $t$ 时刻状态为 $q_i$ 条件下 $t+1$ 时刻后的观测序列为 $o_{t+1},o_{t+2},\cdots,o_T$ 的后向概率 $\beta_t(i)$,只需考虑在 $t+1$ 时刻所有可能的 $N$ 个状态 $q_j$ 的转移概率 $a_{ij}$,在该状态下的观测 $o_{t+1}$ 的观测概率 $b_j(o_{t+1})$,以及在状态 $q_j$ 后的观测序列的后向概率 $\beta_{t+1}(j)$,即有:
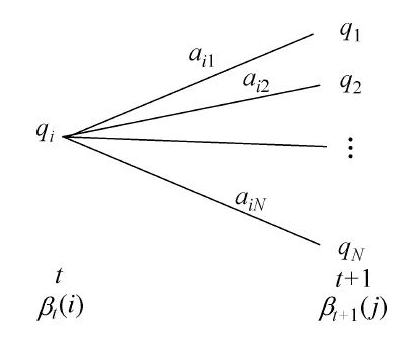
上式即后向概率的递推公式
观测序列概率的计算
由于在 $t=1$ 时刻状态为 $q_i$ 的条件下,从 $2$ 到 $T$ 的部分观测序列为 $o_{2},o_{3},\cdots,o_T$ 的后向概率为:
那么结合初始概率 $\pi_i$ 与观测概率 $b_i(o_1)$,可得到在模型 $\lambda$ 下观测序列 $O$ 出现的概率 $P(O|\lambda)$ 为:
算法流程
综上所述,给出观测序列概率的后向计算法的算法流程
输入:隐马尔可夫模型 $\lambda=(A,B,\pi)$,观测序列 $O=(o_1,o_2,\cdots,o_T)$
输出:观测序列概率 $P(O|\lambda)$
算法步骤如下:
Step 1:算法初始化,对最终时刻 $t=T$ 的所有状态 $q_i$ 规定
Step 2:根据后向概率的递推公式进行递推
对 $t=T-1,T-2,\cdots,1$,有:
Step 3:计算在模型 $\lambda$ 下观测序列 $O$ 出现的概率
【概率与期望值的计算】
前向后向概率递推公式
根据前向概率与后向概率的定义,可以将观测序列概率 $P(O|\lambda)$ 统一写成:
上式即前向后向概率递推公式
当 $t=1$ 时,即为:
当 $t=T-1$ 时,即为:
单一状态计算公式
记 $\gamma_t(i)=P(i_t=q_i|O,\lambda)$ 为在给定模型 $\lambda$ 和观测序列 $O$ 的条件下,在 $t$ 时刻处于状态 $q_i$ 的概率
根据前向概率 $\alpha_t(i)$ 与后向概率 $\beta_t(i)$ 的定义,有:
故有:
双状态计算公式
记 $\xi_t(i,j)=P(i_t=q_t,i_{t+1}=q_j|O,\lambda)$ 为在给定模型 $\lambda$ 和观测序列 $O$ 的条件下,在 $t$ 时刻处于状态 $q_i$ 且在 $t+1$ 时刻处于状态 $q_j$ 的概率
根据前向概率 $\alpha_t(i)$ 与后向概率 $\beta_t(i)$ 的定义,有:
故有:
期望值的计算
将 $\gamma_t(i)$ 和 $\xi_t(i,j)$ 对各个时刻 $t$ 求和,可以得到一些期望值
在观测序列 $O$ 下,状态 $i$ 出现的期望值为:
在观测序列 $O$ 下,由状态 $i$ 转移的期望值为:
在观测序列 $O$ 下,由状态 $i$ 转移到状态 $j$ 的期望值为:

