【欠拟合与过拟合】

当假设空间中含有不同复杂度的模型时，就面临模型选择问题，即假设假设空间中存在符合问题的真模型，那么选择的模型应该逼近该真模型，从而提高预测能力

如果模型复杂度低，在训练集中无法获得足够低的误差，使得模型在训练集上就表现的很差，无法学习到数据背后的规律，这种现象称为欠拟合（Under-fitting）

欠拟合一般会出现于训练刚开始的时候，随着训练次数的增加，欠拟合的现象基本会消失，无需考虑，但如果训练完毕后仍存在欠拟合问题的话，可以在模型中增加特征以解决欠拟合

但如果一味的提高训练集的预测能力，不断地增加模型特征，则会出现过拟合（Over-fitting）现象，即训练误差和测试误差间的差距过大，模型对已知数据的预测表现很好，但对未知数据的预测表现很差的现象

除了增加模型特征使得模型过于复杂导致出现过拟合外，如果训练集样本单一，或者训练数据中噪声干扰过大，仍会出现过拟合现象

如下图，为回归问题中的三种拟合状态

如下图，为分类问题中的三种拟合状态

当模型的复杂度增大时，训练误差会逐渐减小并趋近于 $0$，而测试误差即泛化误差会先减小达到最小值后又增大，因此当选择的模型复杂度过大时，过拟合现象就会发生

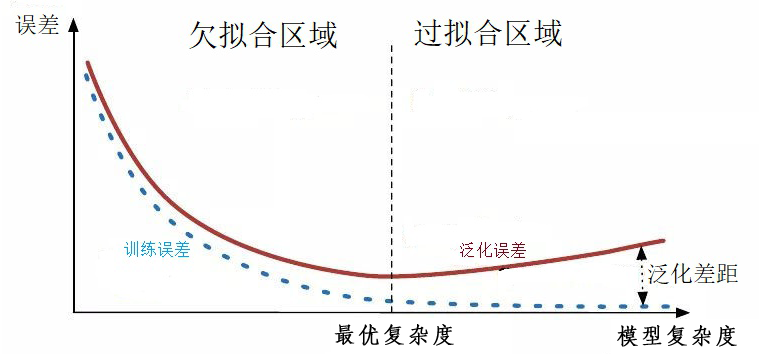
一般而言，解决过拟合问题，就要显著减少测试误差而不过度增加训练误差，从而提高模型的泛化能力

常见的处理方法有：删除冗余特征、正则化（L1/L2 正则化）、交叉验证、自助法、提前终止等

【正则化】

正则化（Regularizatoin）是机器学习的回归问题中最常用的模型选择方法之一，用于选择经验风险与模型复杂度同时较小的模型，其是结构风险最小化策略的实现，即在经验风险的基础上加了一个正则化项（Regularizer），此时损失函数的一般形式如下：

$\min_{f\in\mathcal{F}} \quad \frac{1}{N}\sum_{i=1}^N L(y_i,f(x_i;\boldsymbol{\theta}))+\lambda J(f),\quad \lambda\geq 0$

其中，第一项是经验风险，第二项是正则化项，$\lambda\geq0$ 是用于调整两者之间关系的系数

正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值就越大，在实际应用中，常根据实际模型的情况取模型参数向量的范数（Norm），即利用 L1 范数或 L2 范数作为正则项，进行 L1 正则化或 L2 正则化，从而避免过拟合问题

使用 L1 正则化的回归模型一般称为 Lasso 回归，使用 L2 正则化的回归模型一般称为 Ridge 回归（岭回归）

【交叉验证】

概述

最简单的模型选择方法是随机将数据集分为训练集、验证集、测试集三部分：

训练集（Train Set）：用于训练模型
验证集（Validation Set）：用于模型选择，通过衡量同一个模型的不同参数的表现，选择出一个模型中最好的参数
测试集（Test Set）：用于测试模型，对学习方法进行评估

如果给定的样本数据充足，验证集中有足够多的数据，因此在学习到的不同复杂度的模型中，选择对验证集有最小预测误差的模型即可

在实际应用中，数据可能并不充足，此时可以采用交叉验证（Cross Validation）的方法，将给定数据进行切分，分为训练集、测试集，重复地使用数据来进行训练、选择、测试

样本集比例

在小数据量的时代，如 $100$、$1000$、$10000$ 的数据量大小，可以将数据集按照以下比例进行划分：

无验证集的情况：$7:3$
有验证集的情况：$6:2:2$

在如今的大数据时代，拥有的数据集的规模可能是百万级别的，所以验证集和测试集所占的比重会趋向于变得更小。

100 万数据量：$98 : 1 : 1$
超百万数据量：$99.5: 0.25: 0.25$

简单交叉验证

简单交叉验证首先随机将数据分为训练集、测试集两部分，一般来说，常取 70% 的数据作为训练集，30% 的数据作为测试集

之后用训练集在不同参数个数的条件下训练模型，以得到不同的模型

最后在测试集上对各个模型计算测试误差，选出测试误差最小的模型

S 折交叉验证

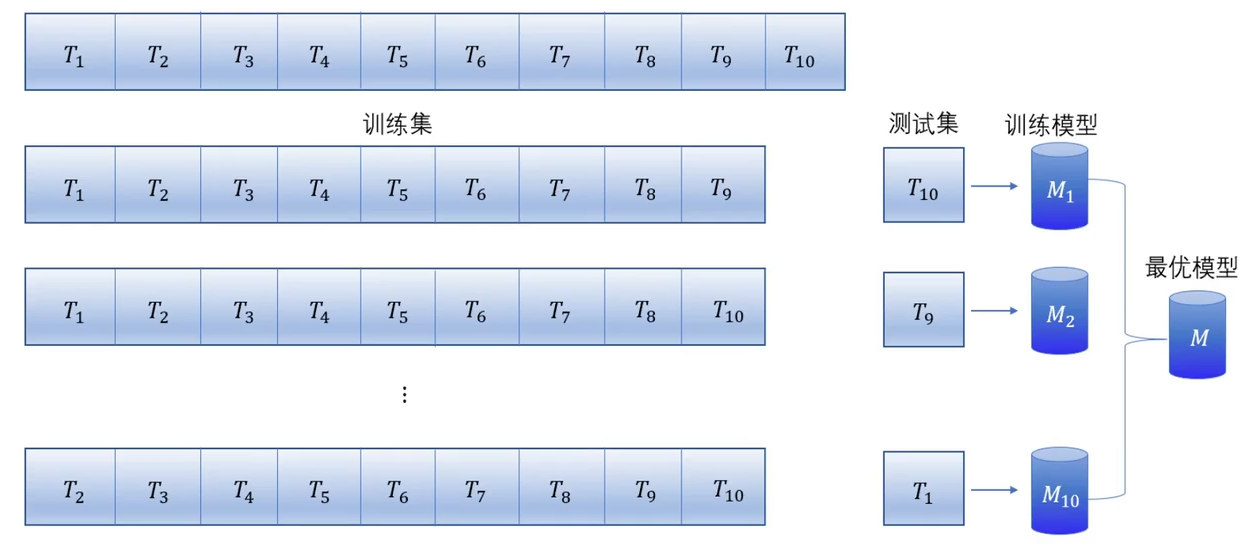
S 折交叉验证（S-fold Cross Validation）是最常用的交叉验证方法，其首先随机将数据分为 $S$ 个互不相交的大小相同的子集，目前一般取 $S=10$，即 10 折交叉验证

之后利用 $S-1$ 个子集的数据训练模型，并利用剩余的 $1$ 个子集测试模型，将训练、测试过程对可能的 $S$ 种选择重复进行

最后选出 $S$ 次评测中平均测试误差最小的模型

留一交叉验证

留一交叉验证（Leave-one-out Cross Validation）是 S 折交叉验证的特殊情形，即对于样本容量为 $N$ 的数据集，取 $S=N$ 的情形

该方法往往在数据极度缺乏的情况下使用

【自助法】

对于一个模型来说，我们希望其能够采用数据集 $D$ 中的全部数据进行训练，但在交叉验证中，无论采用哪种方法，都会保留部分样本进行测试，这使得实际评估的模型使用的训练集要比数据集 $D$ 要小，这就导致会引入一些由于训练样本规模不同造成的估计偏差

为解决上述问题，将推论统计学中的自助采样法（Bootstrap Sampling）引入，从样本统计量来推算总体统计量，这就是自助法（Bootstrapping）

对于给定的包含 $n$ 个样本的初始数据集 $D$，每次随机从 $D$ 中选择一个样本，将其拷贝放入采样数据集 $D’$，放入拷贝的原因是令该样本在下次采样时仍有可能被选择到

将上述过程重复执行 $n$ 次，即得到包含 $n$ 个样本的采样数据集 $D’$，显然，$D$ 中的某些样本会在 $D’$ 中多次出现，某些样本一次也不出现

在 $n$ 次采样中，每个样本被采样的概率是 $\frac{1}{n}$，那么始终不被采样的概率为：

$(1-\frac{1}{n})^n$

取极限有：

$\begin{align*} \lim_{n\rightarrow\infty} (1-\frac{1}{n})^n &= \lim_{n\rightarrow\infty} e^{n\ln (1-\frac{1}{n})} \\ &= e^{n\cdot (-\frac{1}{n})} \\ &= e^{-1} \\ &\approx 0.368 \end{align*}$

即通过自助采样，初始数据集 $D$ 中约有 $36.8\%$ 的样本未出现在采样数据集 $D’$ 中

由此，可将 $D’$ 作为训练集，将 $D\backslash D’$ 作为测试集，即实际评估的模型与期望评估的模型都使用 $n$ 个训练样本，但仍有约 $\frac{1}{3}$ 没有在训练集中出现的数据可以作为测试集

自助法常用于数据量较小，难以划分训练集和测试集的数据集，但自助法产生的数据集改变了初始数据集的分布，会引入估计偏差

【早停止】

早停止（Early Stopping）是一种使用截断迭代次数以防止过拟合的方法，常用于学习过程中存在迭代的学习方法

通常来说，在训练验证的时候，发现过拟合，可以得到如下的损失图

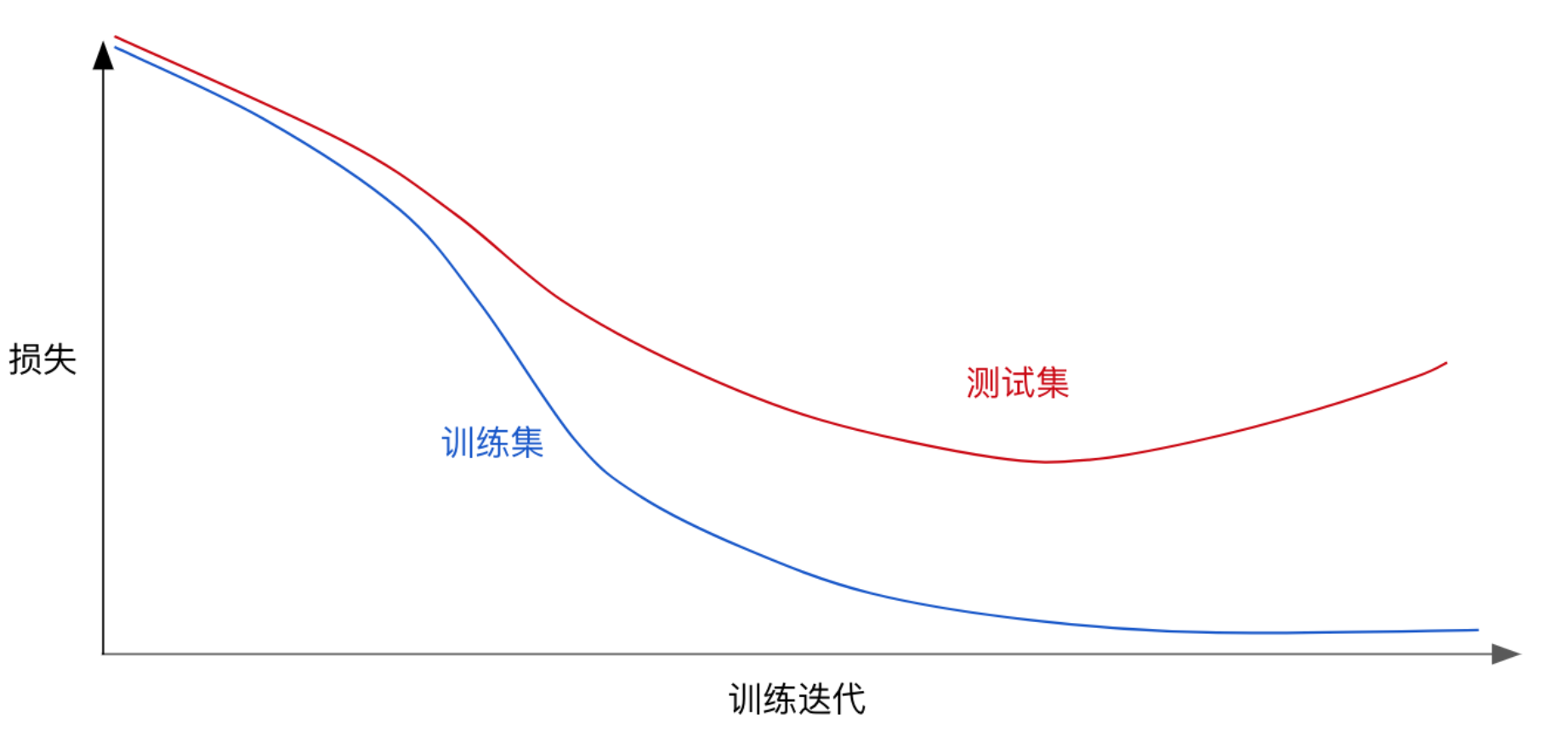
从图中可以看出，在不断训练之后，损失会越来越小，但是到了一定程度后，学习到的模型过于复杂，即过于拟合训练集上的数据的特征，从而造成测试集开始损失较小，后来又变大的情况

那么在模型对训练集迭代收敛前，发现测试集的损失减小到一定程度时，即可停止训练，从而防止过拟合

但早停止这种方法治标不治本，没有从根本上解决数据或模型的问题

Alex_McAvoy

机器学习的模型选择