集成学习结合策略

【结合的好处】

在产生了个体学习器后，需要考虑如何结合这些个体学习器，即结合策略

学习器的结合可能会从三方面带来好处：

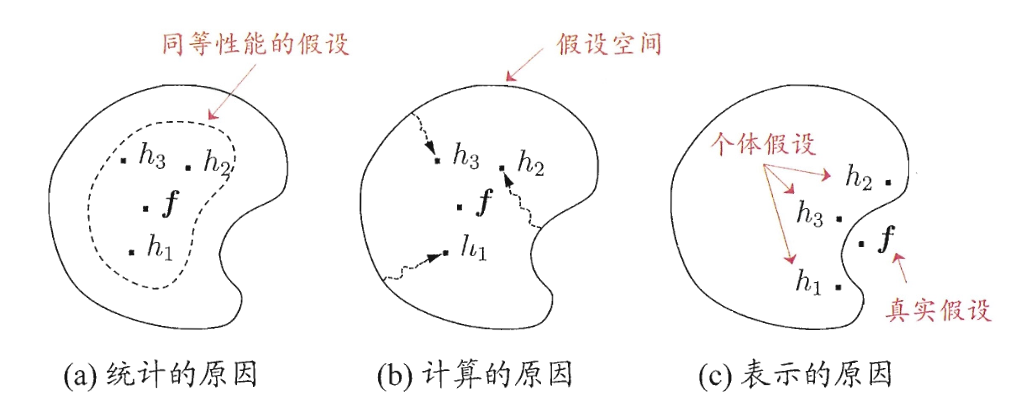
1. 从统计的角度来看，由于学习任务的假设空间往往很大，可能有多个假设在训练集上达到同等性能，此时若使用单学习器可能会因误选而导致泛化性能不佳，使用多个学习器进行结合会减小该风险
2. 从计算的角度来看，学习算法往往会陷入局部极小，有的局部极小点所对应的泛化性能可能会很差，而通过多次运行后进行结合，可降低陷入糟糕的局部极小点的风险
3. 从表示的角度来看，某些学习任务的真实假设可能不在当前学习算法所考虑的假设空间中，此时若使用单学习器则肯定无效，而通过结合多个学习器，会使相应的假设空间有所扩大，可能学得更好的近似

【常见的结合策略】

简单平均法

简单平均法（Simple Averaging）是最简单的一种结合策略，其是将输出结果进行平均，即：

$$H(\mathbf{x}) = \frac{1}{T} \sum_{t=1}^T f_t(\mathbf{x})$$

加强平均法

加权平均法（Weighted Averaging）是集成学习研究的基本出发点，对于给定的个体学习器，不同的集成学习方法可认为通过不同的方式来确定加权平均法中的个体学习器的权重

加权平均是将输出结果进行加权平均，即：

$$H(\mathbf{x}) = \frac{1}{T} \sum_{t=1}^T \omega_tf_t(\mathbf{x})$$

其中，权重 $\omega_t\geq 0, \sum\limits_{t=1}^T \omega_t=1$

权重一般是从训练集中学习而得，在实际应用中，由于训练样本通常不充分或存在噪声，这使得学习出的权重不完全可靠，尤其是对规模较大的集成来说，要学习的权重较多，容易导致过拟合的产生

一般在个体学习器性能相差较大时，使用加权平均法，而在个体学习器性能相近时，则使用简单平均法

此外，可以发现，简单平均是 $\omega_t=\frac{1}{T}$ 的加权平均

投票法

对分类任务来说，个体学习器 $f_t(\mathbf{x})$ 要从类别集合 $\{c_1,c_2,\cdots,c_K\}$ 中预测出一个标记，投票法（Voting）是最常用的结合策略

将 $f_t(\mathbf{x})$ 在样本 $\mathbf{x}$ 上预测的输出表示为一个 $K$ 维向量：

$$(f_t^1(\mathbf{x}),f_t^2(\mathbf{x}),\cdots,f_t^K(\mathbf{x}))$$

其中，$f_t^k(\mathbf{x})$ 表示 $f_t(\mathbf{x})$ 在类别标记 $c_k$ 上的输出

绝对多数投票法（Majority Voting）是当某标记得票过半时，则预测为该标记，否则拒绝预测，即：

$$H(\mathbf{x}) = \left\{\begin{gather*} c_k, && \sum_{t=1}^T f_t^k(\mathbf{x}) > \frac{1}{2}\sum_{k=1}^K\sum_{t=1}^T f_t^k(\mathbf{x}) \\ \text{reject}, && \text{otherwise} \end{gather*}\right.$$

相对多数投票法（Plurality Voting）是预测为得票最多的标记，若同时有多个标记获得最高票，则从中随机选取一个，即：

$$H(\mathbf{x}) = c_{k^*},\quad k^* = \arg\max_{k} \sum_{t=1}^T f_t^k(\mathbf{x})$$

加权投票法（Weighted Voting）与加权平均法类似，其是为每个预测的标记乘以一个权重后，预测加权最大的标记，若同时有多个标记获得最大权，则从中随机选取一个，即：

$$H(\mathbf{x}) = c_{k^*},\quad k^* = \arg\max_{k} \omega_t\sum_{t=1}^T f_t^k(\mathbf{x})$$

其中，权重 $\omega_t\geq 0, \sum\limits_{t=1}^T \omega_t=1$

标准的绝对多数投票法提供了拒绝预测的选择，这在可靠性要求较高的学习任务中是一个很好的机制，但若学习任务要求必须提供预测结果时，绝对多数投票法会退化为相对多数投票法，因此，在不允许拒绝预测的学习任务中，绝对多数、相对多数投票法被统称为多数投票法

此外，上述的三种投票法都没有限制个体学习器输出值的类型，在实际应用中，不同类型的个体学习器 $f_t(\mathbf{x})$ 可能会产生不同类型的 $f_t^k(\mathbf{x})$ 值，例如：

• 类标记：$f_t^k(\mathbf{x})\in \{0,1\}$
• 类概率：$f_t^k(\mathbf{x})\in[0,1]$

使用类标记的投票被称为硬投票（Hard Voting），使用类概率的投票被称为软投票（Soft Voting）

需要注意的是，若个体学习器的类型不同，得到的类概率值不能直接进行比较，通常是将类概率转换为类标记输出后，再进行投票

而且不同类型的 $f_t^k(\mathbf{x})$ 值不能混用，即对一些能在预测出类标记同时产生分类置信度的学习器，其分类置信度可转化为类概率来使用