References:
【概述】
门控循环单元(Gated Recurrent Unit,GRU)是 2014 年 Cho 提出的 LSTM 的一种变体,其在保持了 LSTM 效果同时又简化了结构,使得计算量更小
GRU 对 LSTM 中的输入门、遗忘门、输出门进行改进,简化为两个门
- 更新门(Update Gate):将 LSTM 的遗忘门和输入门进行组合,用于控制前一时间步的状态信息被带入当前时间步的状态的程度,有助于捕捉时间序列里长期的依赖关系
- 重置门(Reset Gate):将 LSTM 的输出门进行改进,用于控制忽略前一时间步的状态信息的程度,有助于捕捉时间序列里短期的依赖关系
同时,其合并了原有的存储单元状态 $c_t$ 和隐藏层状态 $h_t$,极大的简化了循环结构
【GRU 结构】
单个 GRU 的内部结构如下图所示:
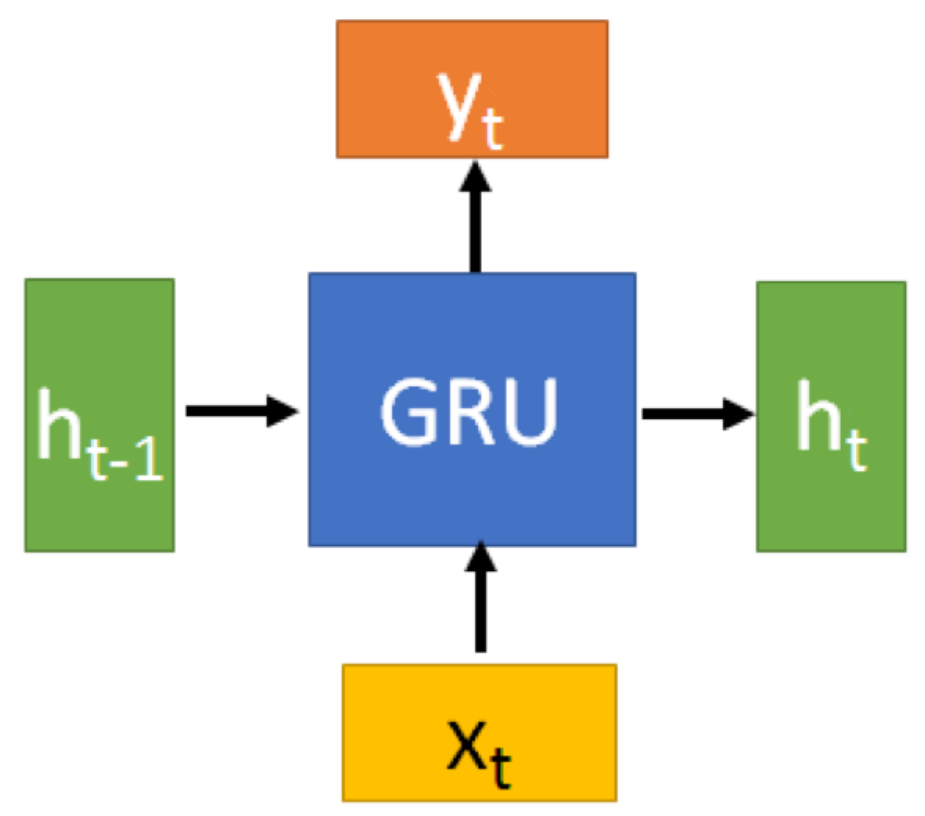
在 RNN 中,只有一个传递状态 $s_t$,在 LSTM 中,有对应于 $s_t$ 的单元状态 $c_t$ 和隐藏状态 $h_t$,到了 GRU 中,又变为了一个状态,即从上一结点传递下来的隐藏状态 $h_t$
在 $t$ 时刻,各符号假设如下:
- $h_t$:$t$ 时刻的 LSTM 单元隐藏输出,即隐藏状态(Hidden State)
- $x_t$:$t$ 时刻的输入数据
【前向传播】
门控状态
GRU 内部使用当前输入 $x_t$ 和上一时间步传递下来的隐藏状态 $h_{t-1}$ 来得到三种状态:$Z$、$R$
$Z$ 是更新门的输出,连接权重矩阵为 $W_z$,偏置项为 $\mathbf{b}_z$,有:
即 $t$ 时刻的输入数据 $x_t$ 与上一时刻 $t-1$ 的隐藏状态 $h_{t-1}$ 经过向量拼接后,与权重矩阵点积后加上偏置项的值,经过 sigmoid 激活函数后,得到一个 $0$ 到 $1$ 间的值,作为一种门控信号,值越大说明前一时刻的状态信息带入的越多
$R$ 是重置门的输出,连接权重矩阵为 $W_r$,偏置项为 $\mathbf{b}_r$,有:
即 $t$ 时刻的输入数据 $x_t$ 与上一时刻 $t-1$ 的隐藏状态 $h_{t-1}$ 经过向量拼接后,与权重矩阵点积后加上偏置项的值,经过 sigmoid 激活函数后,得到一个 $0$ 到 $1$ 间的值,作为一种门控信号,值越大说明前一时刻的状态信息忽略的越多
两个阶段
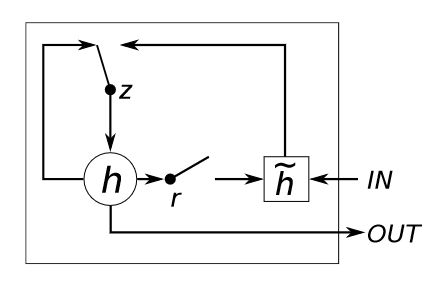
在每个时间步,得到两个门控状态 $Z$、$R$ 后,即进入 GRU 内部的两个阶段
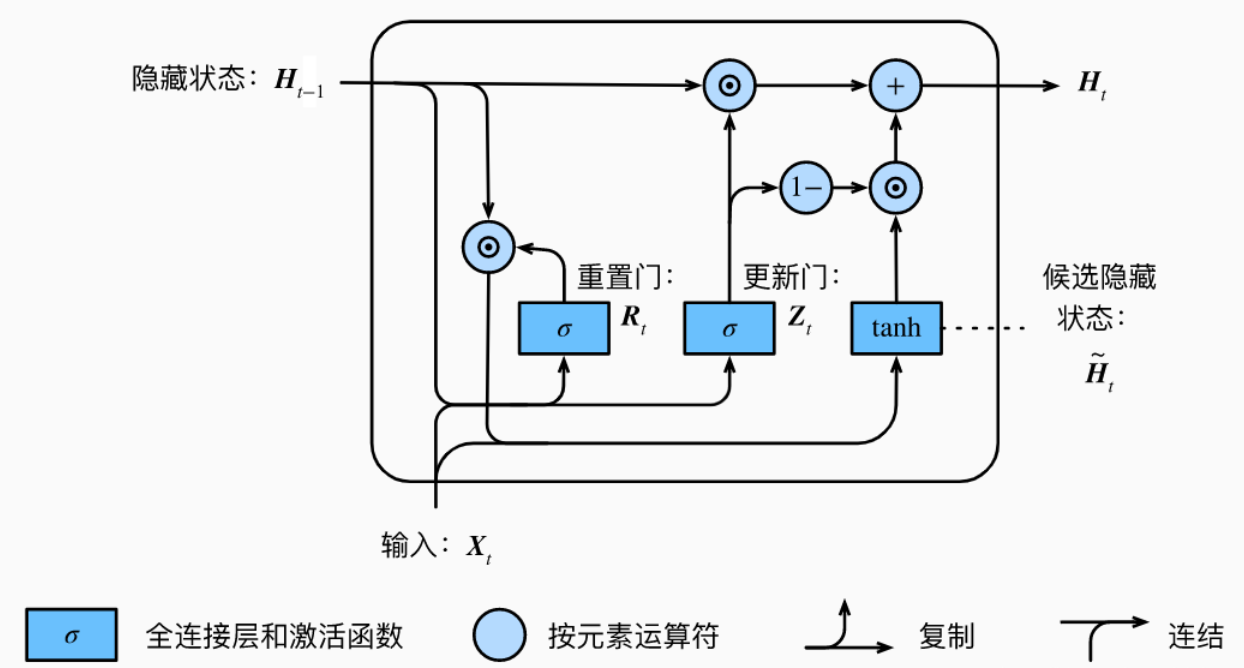
1)候选隐藏状态计算阶段:该阶段利用重置门,对上一时间步隐藏状态 $h_{t-1}$ 进行重置,然后与当前时间步的输入 $x_t$ 计算候选隐藏状态 $h_t’$,类似于 LSTM 中的选择记忆阶段
在得到重置门的门控信号后,首先求上一时间步隐藏状态 $h_{t-1}$ 重置后的数据 $h_{t-1}’$,即:
其中,$\odot$ 为哈达玛积(Hadamard Product),即对相同形状的矩阵中的对应元素相乘
对于重置后的数据 $h_{t-1}’$,将其与 $t$ 时间步的输入数据 $x_t$ 进行拼接,与权重矩阵点积后,再通过一个 tanh 激活函数进行放缩,得到一个 $-1$ 到 $1$ 间的值 $h_t’$
此时的 $h_t’$ 可以看作是当前时刻的新信息,通过重置阶段更新门输出 $R$ 的大小,可以控制其保留了多少之前的记忆,如果 $R=0$,说明 $h_t’$ 只包含当前时间步 $x_t$ 的信息
2)更新记忆阶段:该阶段利用更新门,对当前时间步的候选隐藏状态 $h_t’$ 和上一时间步的隐藏状态 $h_{t-1}$,同时进行遗忘和记忆
在得到更新门的门控信号,根据当前时间步的候选隐藏状态 $h_t’$ 和上一时间步的隐藏状态 $h_{t-1}$,有:
对于更新门的输出 $Z$ 来说,越接近于 $1$,记忆下来的数据就越多,越接近于 $0$,遗忘的数据就越多
值得注意的是,当 $R=0,Z=0$ 时,GRU 退化为一个标准的 RNN

