References：

Backpropagation Through Time: What It Does and How to Do It

详解循环神经网络(Recurrent Neural Network

时序反向传播算法(BPTT)

BPTT算法推导

【概述】

RNN 是一种基于时序数据的神经网络模型，根据其前向传播公式可知，优化的目标是计算损失函数关于参数 $U$、$V$、$W$ 以及两个偏置 $\mathbf{b}_o$、$\mathbf{b}_h$ 的梯度，然后使用梯度下降法学习出好的参数

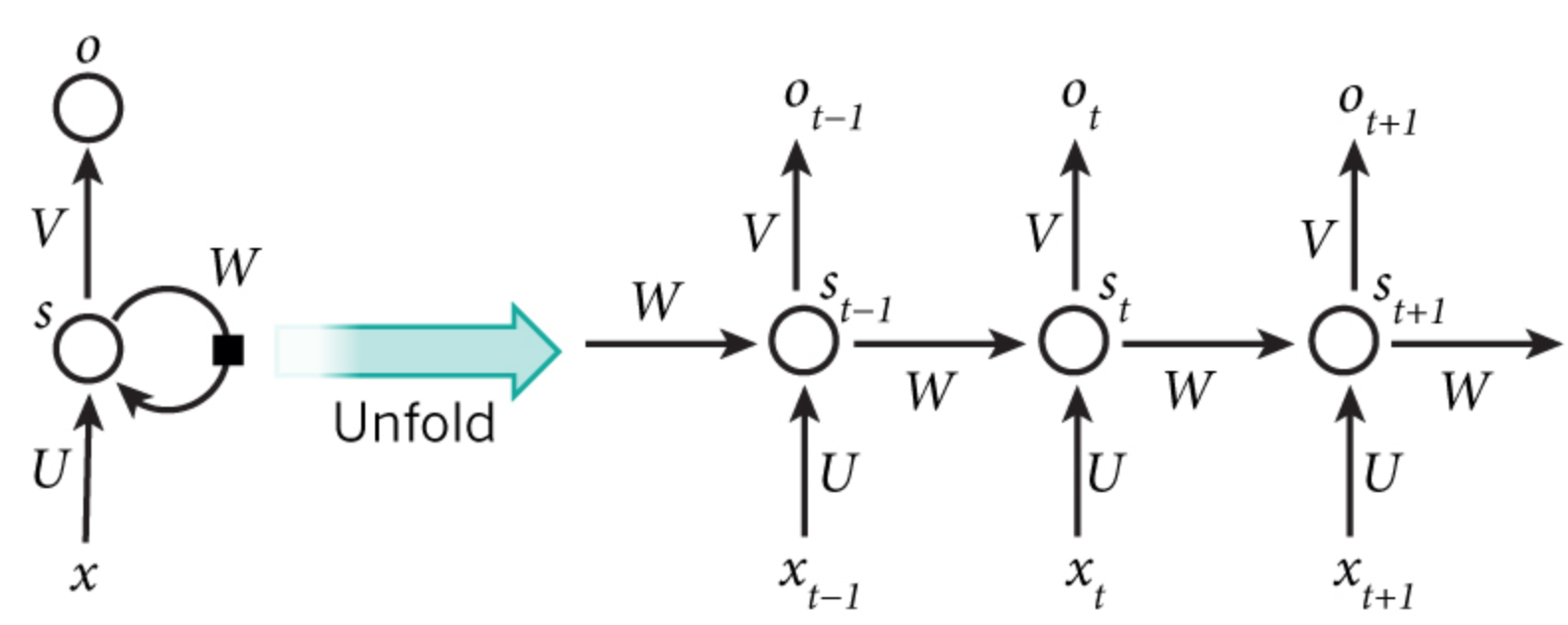
$\begin{gather*} s_t = f(U\cdot x_t + W\cdot s_{t-1} + \mathbf{b}_h) \\ o_t = g(V\cdot s_t+\mathbf{b}_o) \end{gather*}$

由于参数是共享的，因此需要将训练实例在每个时刻的梯度相加，然后进行更新

以下图为例，对于 $U$、$W$、$\mathbf{b}_h$，在需要梯度更新时，需要将每个时间 $t=0$、$t=1$、$t=2$、$t=3$、$t=4$ 的梯度 $\frac{\partial s_t}{\partial U}$ 、$\frac{\partial s_t}{\partial W}$、$\frac{\partial s_t}{\partial \mathbf{b}_h}$ 计算出来，然后将加起来的梯度作为总的更新梯度

传统的 BP 算法无法解决该问题，为此 Mikolov 提出了时序反向传播算法（Back-Propagation Through Time，BPTT）

其按照时间序列将 RNN 展开，展开后的网络包含 N（时间步长）个隐含单元和一个输出单元，然后采用反向误差传播方式对神经网络的连接权值进行更新

【算法原理】

符号假设

假设 RNN 隐藏层的激活函数 $f(\cdot)$ 为 tanh 函数，输出层激活函数为 softmax 函数，损失函数采用交叉熵损失函数 $E(y_i,\hat{y}_i)=-y_i\log \hat{y}_i$，$t$ 时刻的输出标签为 $y_t$，那么有：

$\left\{\begin{align*} s_t &= \tanh(U\cdot x_{t} + W\cdot s_{t-1}+\mathbf{b}_h) \\ o_t &= \text{softmax} (V\cdot s_t +\mathbf{b}_o) \\ E_t &= -y_t\log(o_t) \\ E &= \sum_{t}^T E_t \end{align*}\right.$

更新梯度

从 RNN 的循环单元结构来说，对于每个循环单元，均需计算 $t$ 时刻当前层损失 $E_t$ 对于当前隐层状态输出值 $s_t$ 的梯度，即：$\frac{\partial E_t}{\partial s_t}=ds_t$

除最后一个循环单元，其他的循环单元还需计算后一层梯度 $ds_t$ 对于当前层梯度 $ds_{t-1}$ 的梯度，即： $\frac{ds_{t+1}}{ds_{t}}$

因此，最终各循环单元的更新梯度为：

最后一个循环单元：$\frac{\partial E}{\partial s_t}=ds_t$
除最后一个循环单元的其他单元：$ds_t+\frac{ds_{t+1}}{ds_{t}}$

以下图为例，对于最后一个循环单元 $\text{E}4$，其只需计算 $t=4$ 时刻当前层损失 $\text{E}4$ 对于当前隐层状态输出值 $s_4$ 的梯度 $ds_4$

对于其他的循环单元 $\text{E}_i,i=0,1,2,3$，除了计算当前层梯度 $ds_i$ 外，还需计算后一层梯度对当前层梯度的梯度 $\frac{ds_{i+1}}{ds_i}$

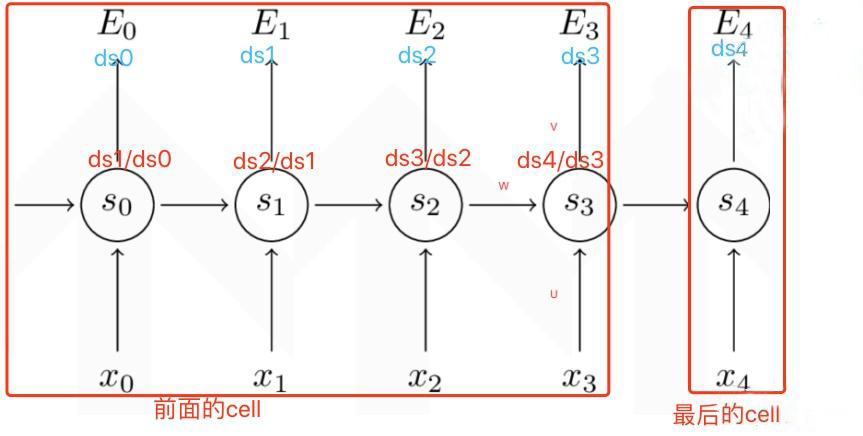
循环单元内部的梯度

激活函数的导数

对于 RNN 中的 $t$ 时刻的隐藏层状态输出为：

$s_t= \tanh(U\cdot x_{t} + W\cdot s_{t-1}+\mathbf{b}_h)$

同时，$t$ 时刻当前层损失 $E_t$ 对于隐藏层状态输出 $s_t$ 的梯度是 $\frac{\partial E_t}{\partial s_t}=ds_t$

考虑到激活函数 $\tanh(\cdot)$，其导数为 $1-\tanh^2(\cdot)$，因此，先求损失函数对激活函数的导数，令 $\mathbf{x}=U\cdot x_{t} + W\cdot s_{t-1}+\mathbf{b}_h$，则有 $s_t=\tanh(\mathbf{x})$，故：

$\begin{align*} \frac{\partial E_t}{\partial \mathbf{x}} &= \frac{\partial E_t}{\partial s_t}\cdot \frac{\partial s_t}{\partial \mathbf{x}} \\ &= ds_t \cdot \frac{\partial \tanh(\mathbf{x})}{\partial \mathbf{x}}\Big( \tanh(x)\Big) \\ &= ds_t\cdot(1-\tanh^2(\mathbf{x})) \\ &= (1-s_t^2)ds_t \end{align*}$

$U$、$W$、$\mathbf{b}_h$ 的导数

对于每个循环单元内部的 $U$、$W$、$\mathbf{b}_h$ 进行更新时，需要损失函数对它们的各时刻的导数

令 $\mathbf{x}=U\cdot x_{t} + W\cdot s_{t-1}+\mathbf{b}_h$，有 $s_t=\tanh(\mathbf{x})$

可得 $t$ 时刻损失函数 $E_t$ 对激活函数 $\tanh(\cdot)$ 的导数为：

$\frac{\partial E_t}{\partial \mathbf{x}}=(1-s_t^2)ds_t$

那么，$t$ 时刻当前层损失 $E_t$ 对输入层的连接权重矩阵 $U$ 的导数为：

$\begin{align*} \frac{\partial E_t}{\partial U} &= \frac{\partial E_t}{\partial \mathbf{x}} \cdot \frac{\partial \mathbf{x}}{\partial U} \\ &=(1-s_t^2)ds_t\cdot x_t \end{align*}$

$t$ 时刻当前层损失 $E_t$ 对从 $t-1$ 时刻到 $t$ 时刻的隐藏层连接权重矩阵 $W$ 的导数为：

$\begin{align*} \frac{\partial E_t}{\partial W} &= \frac{\partial E_t}{\partial \mathbf{x}} \cdot \frac{\partial \mathbf{x}}{\partial W} \\ &=(1-s_t^2)ds_t\cdot x_{t-1} \end{align*}$

$t$ 时刻当前层损失 $E_t$ 对隐藏层的偏置向量 $\mathbf{b}_h$ 的导数为：

$\begin{align*} \frac{\partial E_t}{\partial \mathbf{b}_h} &= \frac{\partial E_t}{\partial \mathbf{x}} \cdot \frac{\partial \mathbf{x}}{\partial \mathbf{b}_h} \\ &=\sum (1-s_t^2)ds_t \end{align*}$

$x_t$ 与 $s_{t-1}$ 导数

对于循环单元之间反向传播，需要损失函数对 $x_t$ 与 $s_{t-1}$ 的导数

令 $\mathbf{x}=U\cdot x_{t} + W\cdot s_{t-1}+\mathbf{b}_h$，有 $s_t=\tanh(\mathbf{x})$

可得 $t$ 时刻损失函数 $E_t$ 对激活函数 $\tanh(\cdot)$ 的导数为：

$\frac{\partial E_t}{\partial \mathbf{x}}=(1-s_t^2)ds_t$

那么，$t$ 时刻当前层损失 $E_t$ 对输入 $x_t$ 的导数为：

$\begin{align*} \frac{\partial E_t}{\partial x_t} &= \frac{\partial E_t}{\partial \mathbf{x}} \cdot \frac{\partial \mathbf{x}}{\partial x_t} \\ &=U (1-s_t^2)ds_t \end{align*}$

$t$ 时刻当前层损失 $E_t$ 对 $t-1$ 时刻隐藏层输出 $s_{t-1}$ 的导数为：

$\begin{align*} \frac{\partial E_t}{\partial s_{t-1}} &= \frac{\partial E_t}{\partial \mathbf{x}} \cdot \frac{\partial \mathbf{x}}{\partial s_{t-1}} \\ &=W (1-s_t^2)ds_t \end{align*}$

Alex_McAvoy

时序反向传播算法 BPTT