图神经网络 GNN

【概述】

随着机器学习、深度学习的发展，语音、图像、自然语言处理逐渐取得了很大的突破，语音、图像、文本都是简单的序列或网格数据，深度学习很擅长处理该类的结构化数据

但现实世界中并非所有事物都是结构化数据，即并非都可以表示为一个序列或者一个网络，例如社交网络、知识图谱、复杂的文件系统等

相比于简单的文本、图像，这种网络类型的非结构化数据十分复杂，处理这类数据的难点包括：

1. 图的大小是任意的，且拓扑结构复杂，没有像图像一样的空间局部性
2. 图没有固定的结点顺序，即没有一个参考结点
3. 图通常是动态图，且包括多模态特征

针对这类非结构化数据的处理和建模，Franco Scarselli 等人首次在《The Graph Neural Network Model》中提出了图神经网络（Graph Neural Network Model，GNN），将神经网络应用在图数据结构上，并详细叙述了网络模型的结构组成、计算方法、优化算法、流程实现等

其基本思想是基于信息传播机制，在每一个结点通过相互交互信息来更新自己的结点状态，直到达到某一稳定值，输出就是在每个结点处，根据当前结点状态分别计算输出

【图领域应用】

对于机器学习中的图领域问题，假设函数 $\tau$ 是一个将图 $G$ 和图中一个结点 $n$ 转换为一个实值 $m$ 维向量的函数：

$$\tau(G,n) \in \mathbb{R}^{m}$$

那么机器学习的任务就在于从已知样本中学习得到这样的函数

图领域的应用主要可以分为两种类型：

1. 专注于图的应用（Graph-focused）：函数 $\tau$ 和具体的结点无关，即 $\tau(G)$，训练时在图数据集中进行分类或回归
2. 专注于结点的应用（Node-focused）：函数 $\tau$ 依赖于具体的结点 $n$，即 $\tau(G,n)$，分类或回归取决于每个结点的属性

如下图所示：

• 图 a 是化学分支结构，能够用图 $G$ 表示，函数 $\tau(G)$ 可能用于估计这种化学分子对人有害的概率，因此不关注分子中具体原子（结点），所以属于 Graph-focused
• 图 b 是城堡图片，图中每一种结构都由结点表示，函数 $\tau(G,n)$ 可能用于预测每一个结点是否属于城堡，所以属于 Node-focused
• 图 c 是网页分类，图中每一个网页都代表一个结点，函数 $\tau(G,n)$ 可能用于预测网页分类，所以属于 Node-focused

【模型】

符号假设

• 图 $G$ 表示为：$G(N,E)$，其中 $N$ 为结点集，$E$ 为边集
• $\text{ne}[n]$ 表示结点 $n$ 的邻居集合
• $\text{co}[n]$ 表示以结点 $n$ 为顶点的边集
• $\mathbf{l}_n\in \mathbb{R}^{l_N}$ 表示结点 $n$ 的特征向量
• $\mathbf{l}_{(n_1,n_2)}\in\mathbb{R}^{l_E}$ 表示边 $(n_1,n_2)$ 的特征向量
• $\mathbf{l}$ 表示所有特征向量堆叠在一起的向量

考虑图可以是位置图（Positional Graph）也可以非位置图（Non-positional Graph），对于位置图来说，对于每一个结点 $n$，都会给该结点的邻居结点 $u$ 赋予一个位置值 $v_n(u)$，该值是一个单射函数，即：

$$v_n: \text{ne}[n] \rightarrow \{1,2,\cdots,|N|\}$$

假设存在一个图-结点对的集合 $\mathcal{D}=\mathcal{G}\times \mathcal{N}$，$\mathcal{G}$ 为图的集合，$\mathcal{N}$ 为结点集合，那么图领域问题可以表示为有如下数据集的监督学习框架：

$$\mathcal{L} = \{ (G_i,n_{ij},\mathbf{t}_{ij}) | G_i=(N_i,E_i)\in\mathcal{G};n_{ij}\in N_{i};\mathbf{t}_{ij}\in\mathbb{R}^m;1\leq i\leq p,1\leq j \leq q_i \}$$

其中，$n_{ij}\in N_i$ 表示集合 $N_i \in \mathcal{N}$ 中的第 $j$ 个结点，$\mathbf{t}_{ij}$ 表示结点 $n_{ij}$ 的期望目标（标签），$p\leq |\mathcal{G}|,q_{i}\leq |\mathcal{N_i}|$

模型表示

对于图中的结点 $n$，其状态用 $\mathbf{x}_n\in \mathbb{R}^s$ 表示，输出用 $\mathbf{o}_n$ 表示，那么状态和输出可以表示为：

$$\begin{gather*} \mathbf{x}_n = f_w(\mathbf{l}_n,\mathbf{l}_{\text{co}[n]},\mathbf{x}_{\text{ne}[n]},\mathbf{l}_{\text{ne}[n]}) \\ \mathbf{o}_n = g_w(\mathbf{x}_n,\mathbf{l}_n) \end{gather*}$$

其中，$f_w$ 被称为局部转移函数（Local Transition Function），其表达了结点对其领域的依赖关系，$g_w$ 被称为局部输出函数（Local Output Function），其描述了输出如何产生的，$\mathbf{l}_n$ 是结点 $n$ 的特征向量，$\mathbf{l}_{\text{co}[n]}$ 是以结点 $n$ 为顶点的边的特征向量，$\mathbf{x}_{\text{ne}[n]}$ 是结点 $n$ 的邻居结点的状态，$\mathbf{l}_{\text{ne}}[n]$ 是结点 $n$ 的邻居结点的特征向量

令 $\mathbf{x},\mathbf{o},\mathbf{l},\mathbf{l}_N$ 表示所有结点的状态、输出、特征向量、所有结点特征向量叠加构造的向量，那么上式可写为：

$$\mathbf{x} = F_w(\mathbf{x},\mathbf{l}) \\ \mathbf{o} = G_w(\mathbf{x},\mathbf{l}_N)$$

其中，$F_w$ 被称为全局转移函数（Global Transition Function），$G_w$ 被称为全局输出函数（Global Output Function），分别是 $|N|$ 个 $f_w$ 和 $g_w$ 的叠加

综上可以发现，要实现 GNN 模型，必须提供以下三项：

1. 求解状态 $\mathbf{x}_n$ 和输出 $\mathbf{o}_n$ 的方法
2. 学习算法
3. 转换和输出功能的实现，即局部转移函数 $f_w$ 和局部输出函数 $g_w$

状态计算

根据 Banach 的不动点理论，假设 $F_w$ 是一个压缩映射函数，那么上式有唯一不动点解，且可以通过迭代方式逼近该不动点

$$\mathbf{x}(t+1) = F_w(\mathbf{x},\mathbf{l})$$

其中，$\mathbf{x}(t)$ 表示 $\mathbf{x}$ 在第 $t$ 个迭代时刻的值

对于任意初值，迭代的误差是以指数速度减小的，使用迭代的形式可以写出状态和输出的更新表达式：

$$\begin{gather*} \mathbf{x}_n(t+1)=f_w(\mathbf{l}_n,\mathbf{l}_{\text{co}[n]},\mathbf{x}_{\text{ne}[n]}(t),\mathbf{l}_{\text{ne}[n]}) \\ \mathbf{o}_n(t) = g_w(\mathbf{x}_n(t),\mathbf{l}_n),&n\in N \end{gather*}$$

上述的更新表达式可以理解为由单元组成的网络表示，这样的网络被称为编码网络（Encoding Network）

为构建编码网络，图中的每个结点被函数 $f_w$ 的单元代替，每个单元存储当前结点 $n$ 的状态 $\mathbf{x}_n(t)$，在激活时，利用结点的特征向量和邻居结点中的信息去计算新的状态 $\mathbf{x}_n(t+1)$，结点 $n$ 的输出由另一个单元 $g_w$ 产生

如下图所示，顶端的图是原始图，中间的图表示状态向量和输出向量的计算流图，底端的图表示将更新流程迭代 $T$ 次并展开后得到的等效网络图

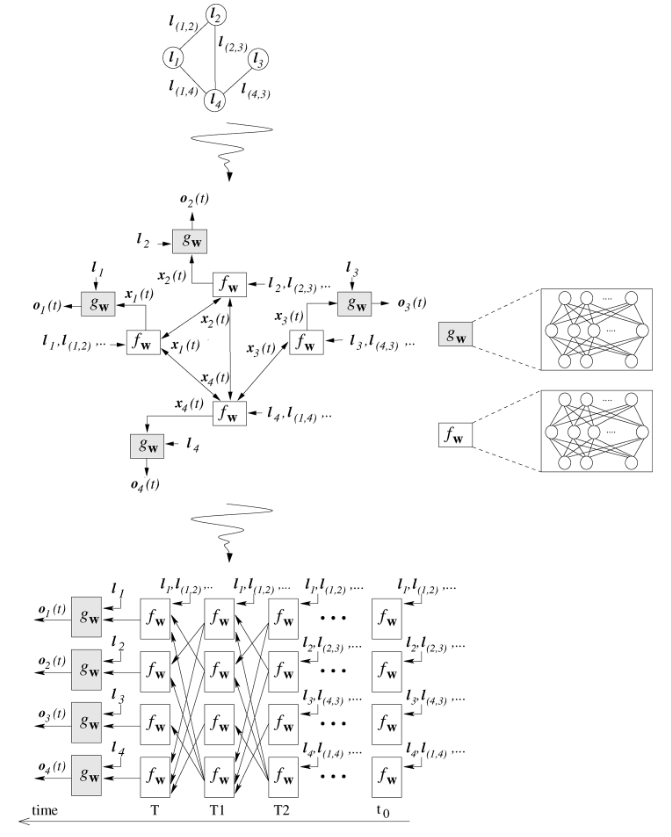
学习算法

GNN 的学习就是估计参数 $w$，使得函数 $\varphi_w$ 能够近似估计训练集：

$$\mathcal{L} = \{ (G_i,n_{ij},\mathbf{t}_{ij}) | G_i=(N_i,E_i)\in\mathcal{G};n_{ij}\in N_{i};\mathbf{t}_{ij}\in\mathbb{R}^m;1\leq i\leq p,1\leq j \leq q_i \}$$

其中，$q_i$ 是图 $G_i$ 中监督学习的结点个数，对于 Graph-focused 的任务，需要增加一个特殊结点 $q_i=1$，该结点用于作为目标结点，从而使得 Graph-focused 任务和 Node-focused 任务统一到结点预测任务上

学习任务可以表示为如下的二次损失函数的最小化：

$$e_{w} = \sum_{i=1}^p\sum_{j=1}^{q_i} (\mathbf{t}_{ij}-\varphi(G_i,n_{ij}))^2$$

优化算法基于随机梯度下降法，按照如下步骤进行：

1. 按照迭代方程进行迭代，更新状态 $\mathbf{x}_n(t)$，直到 $T$ 时刻逼近不动点解 $\mathbf{x}(T)\approx \mathbf{x}$
2. 计算参数权重的梯度 $\frac{\partial e_w(T)}{\partial w}$
3. 根据梯度更新权重

算法流程图如下，其中 FORWARD 用于迭代计算出收敛点，BACKWARD 用于计算梯度

转换和输出功能

在 GNN 中，局部输出函数 $g_w$ 不需要满足特定约束，直接使用多层前馈网络即可，而局部转移函数 $f_w$ 由于需要满足压缩映射的条件，且与不动点计算相关，因此需要着重考虑

Linear GNN

对于结点状态的计算，将 $\mathbf{x}_n = f_w(\mathbf{l}_n,\mathbf{l}_{\text{co}[n]},\mathbf{x}_{\text{ne}[n]},\mathbf{l}_{\text{ne}[n]})$ 中的 $f_w$ 改为如下形式：

$$\mathbf{x}_n = \sum_{u\in \text{ne}[n]} h_w (\mathbf{l}_n,\mathbf{l}_{(n,u)},\mathbf{x}_u,\mathbf{l}_u), \quad n\in N$$

相当于是对结点 $n$ 的邻居结点使用函数 $h_w$，并将得到的值求和作为结点 $n$ 的状态，由此，可按如下方式实现：

$$h_w(\mathbf{l}_n,\mathbf{l}_{(n,u)},\mathbf{x}_u,\mathbf{l}_u) = A_{nu}\mathbf{x}_u + \mathbf{b}_n$$

其中，向量 $\mathbf{b}_n\in \mathbb{R}^s$，矩阵 $A_{nu}\in \mathbb{R}^{s\times s}$，定义为两个前馈神经网络的输出

更准确来说，产生矩阵 $A_{nu}$ 的前馈网络是过渡网络（Transition Network），产生向量 $\mathbf{b}_n$ 的前馈网络是强迫网络（Forcing Network）

由于过渡网络 $\phi_w$ 和强迫网络 $\rho_w$ 分别可以表示为：

$$\begin{gather*} \phi_w:\mathbb{R}^{2\mathbf{l}_N+\mathbf{l}_E} \rightarrow \mathbb{R}^{s^2} \\ \rho_w:\mathbb{R}^{\mathbf{l}_n} \rightarrow \mathbb{R}^s \end{gather*}$$

那么由此就可以定义矩阵 $A_{nu}$ 和向量 $\mathbf{b}_n$，即：

$$\begin{gather*} A_{nu} = \frac{\mu}{s| \text{ne}[u] |} \cdot \Xi \\ \mathbf{b}_n = \rho_w(\mathbf{l}_n) \end{gather*}$$

其中，$\mu\in (0,1),\Xi=\text{resize}(\phi_w(\mathbf{l}_n,\mathbf{l}_{(n,u)},\mathbf{l}_u))$，$\text{resize}(\cdot)$ 表示将 $s^2$ 维向量 reshape 成 $s\times s$ 的矩阵

简单来说，就是将过渡网络的输出 reshape 成方形矩阵，然后乘以一个系数 $\frac{\mu}{s| \text{ne}[u] |}$ 即得到矩阵 $A_{nu}$，向量 $\mathbf{b}_n$ 直接就是强迫矩阵的输出

Non-linear GNN

对于非线性 GNN 来说，$h_w$ 通过多层前馈网络实现，但不是所有的参数 $w$ 都会被使用，因为需要保证 $F_w$ 是一个压缩映射函数，这可以通过惩罚项来实现：

$$e_w = \sum_{i=1}^p \sum_{j=1}^{q_i} (\mathbf{t}_{ij}-\varphi_w(G_i,n_{ij}))^2 +\beta L(\Vert\frac{\partial F_w}{\partial \mathbf{x}}\Vert)$$

其中，惩罚项 $L(y)$ 在 $y>\mu$ 时为 $(y-\mu)^2$，在 $y\leq \mu$ 时为 $0$，参数 $\mu\in(0,1)$ 被定义为期望的 $F_w$ 的压缩系数