生成对抗网络 GAN

【概述】

机器学习的模型可分为判别式模型和生成式模型两大类，由于反向传播、Dropout 等算法的出现，基于深度学习的判别式模型得到迅速发展，而由于生成式模型建模较为困难，因此发展缓慢，直到生成对抗网络（Generative Adversarial Network，GAN）的出现，这一领域才重新开始焕发生机

GAN 模型的主要结构包括一个生成器（Generator）和一个判别器（Discriminator），通过两者的互相博弈学习产生输出，具体来说，生成器 G 的任务是生成看起来自然真实的、与原始数据相似的样本，判别器 D 的任务是判定给定的样本是来源于真实数据集的，还是来源于生成模型伪造的

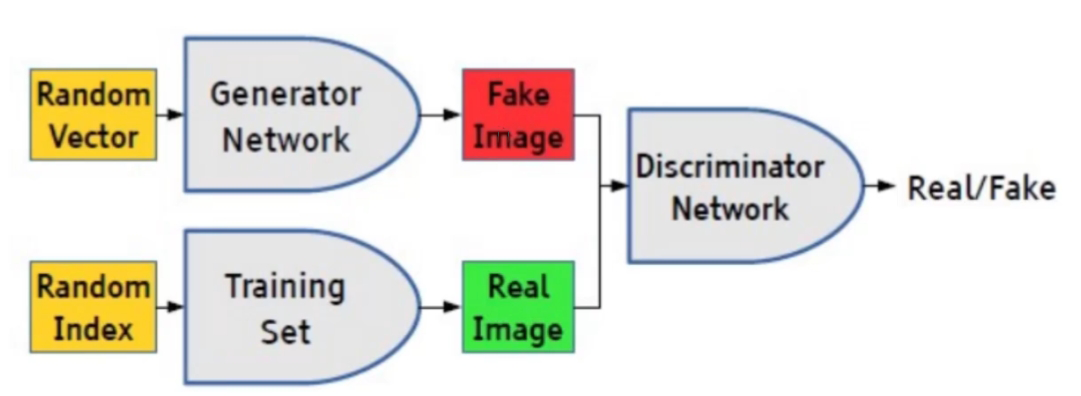
这可以看做一种零和博弈，生成器像一个造假团伙，试图生产和使用假币，而判别器像检测假币的警察。生成器试图欺骗判别器，判别器则努力不被生成器欺骗。模型经过交替优化训练，两种模型都能得到提升，但最终得到的是效果提升到很好的生成器，这个生成器所生成的产品能达到真假难分的地步

目前，GAN 的应用场景主要有：

1. 图像数据增强，利用 GAN 生成图像数据
2. 图像降噪修复、超分辨率重构、图像风格迁移等
3. 与强化学习结合，将 GAN 应用于离散数据

【网络结构】

在原始的 GAN 理论中，并不要求生成器 G 和判别器 D 都是神经网络，只要是能够拟合相应生成和判别的可微分函数即可，但在实际应用中，一般都采用深度神经网络作为生成器 G 和判别器 D

GAN 的基本结构如下图所示，其是由生成器 G 和判别器 D 两个网络组合而成，对于生成器 G 来说，其输入为随机噪声向量 $z$，输出为给定像素大小的图像 $G(z)$，对于判别器 D 来说，其是一个判别网络，即判别给定的输入图片 $x$ 是不是真实的，输出 $D(x)$ 代表 $x$ 为真实的概率

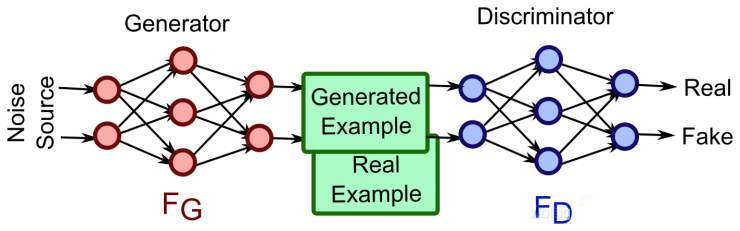
具体来说，生成器可以是任意输出图像的模型，通常采用最简单的全连接神经网络，以防止网络层次太深导致梯度消失或者梯度爆炸，输入向量可以视为携带输出的某些信息，由于对于输出没有具体要求，只要求其能够最大程度的与真实数据相似，从而骗过判别器，因此使用随机噪声的作为输入向量即可

判别器 $D$ 判别的是输入图像 $x$ 的真伪，并不需要判别 $x$ 究竟是什么，只需要判别 $x$ 是来自于真实数据集，还是来自于生成器生成的图像 $G(z)$​，因此只需要输出一个概率即可

【训练流程】

综上所述，GAN 就是生成器 G 和判别器 D 两个网络的叠加组合，其核心思想可以简单的概况为：令生成器 G 学习真实数据集中样本分布，期望生成分布能够拟合于数据的真实分布，并且判别器分辨不出样本是真实的还是生成的

整个 GAN 的训练过程可分为如下四步：

1. 参数初始化：初始化生成器参数 $\theta_{g}$ 和判别器参数 $\theta_d$
2. 采样：从真实数据集中采样 $n$ 个样本 $\{x_1,x_2,\cdots,x_n\}$，从先验分布噪声中采样 $n$ 个噪声样本 $\{z_1,z_2,\cdots,z_n\}$，并利用噪声样本生成对应的生成样本 $\{\tilde{x}_1,\tilde{x}_2,\cdots,\tilde{x}_n\}$
3. 训练判别器 D：固定生成器 $G$，对判别器进行 $k$ 次训练，使其能够尽可能地区分生成样本和真实样本
4. 训练生成器 G：选择较小的学习率对生成器 G 进行 $1$ 次训练 ，使其能够尽可能地减小生成样本与真实样本间的差距，即尽量使判别器 D 判别错误

多次更新迭代后，最终理想情况是使得判别器 D 判别不出样本来自于生成器的输出还是真实训练集，即最终样本判别概率为 $0.5$​

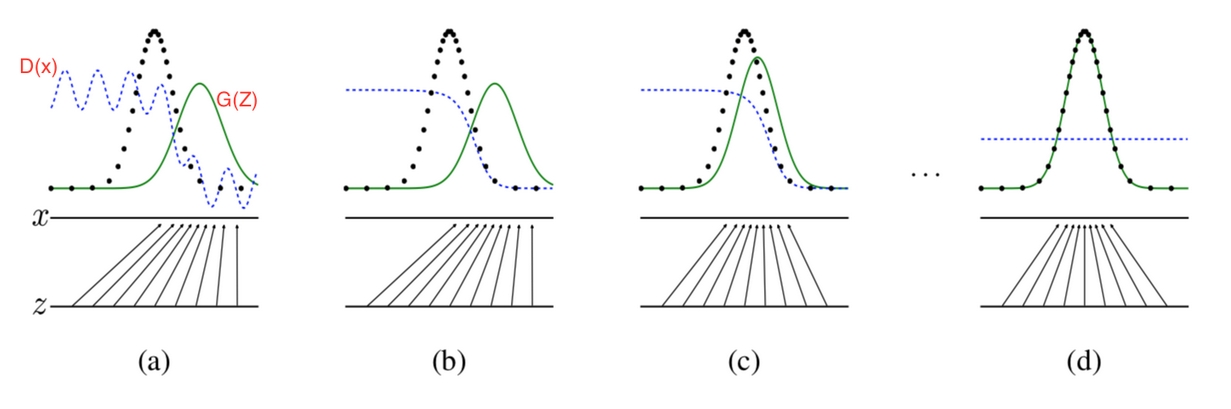
整个过程可表现为上图的四个状态，其中黑色虚线为真实样本分布，绿色实线为生成样本分布，蓝色虚线为生成样本在判别器中的判别概率分布，$z$ 为随机噪声，$z$ 到 $x$ 的映射为生成器生成的分布映射

1. 初始状态 $(a)$：最初始的状态，生成器的生成分布和数据的真实分布区别很大，并且判别器判别出样本的概率不稳定
2. 判别器状态 $(b)$：经过 $k$ 次训练判别器后，判别器达到该状态，此时判别样本区分得非常显著
3. 生成器状态 $(c)$：经过 $1$ 次训练生成器后，生成器达到该状态，此时生成器的生成分布逼近了数据的真实分布
4. 理想状态 $(d)$​：最终希望到达的状态，生成器的生成分布拟合于数据的真实分布，并且判别器分辨不出样本是生成的还是真实的

需要注意的是，之所以要先训练 $k$ 次判别器 D，再训练生成器 G，是因为要先拥有一个好的判别器 D，使得能够教好地区分出真实样本和生成样本之后，才好更为准确地对生成器 G 进行更新

【损失函数】

对于 GAN 来说，其有生成器 G 和判别器 D 两个网络，优化目标即寻找两个网络间的纳什均衡（对于博弈中的每个参与者，只要其他人不改变策略，他就无法改善自己的状况），即生成器 G 的生成分布拟合于数据的真实分布，使得判别器 D 判别不出样本来自于生成器的输出还是真实训练集，即最终样本判别概率为 $0.5$

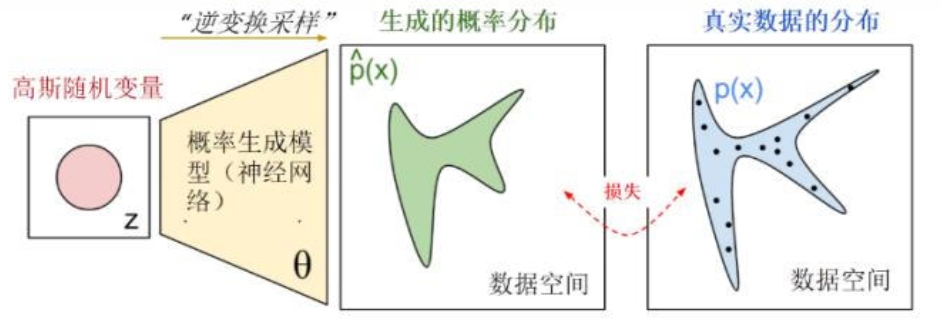
由于 GAN 关心的是生成分布和真实分布间的差异，而对于两种概率分布的差异，通常使用交叉熵来表达，即：

$$\mathbb{H}(p,q)=-\sum_{i} p_i \log q_i$$

对于 GAN 中的样本点，其有两个出处：

1. 真实样本 $x$
2. 生成器的生成样本 $\tilde{x}\sim G(z)$

其中，对于真实样本，要判别其为正确的分布 $y_i$，对于生成样本 $\tilde{x}$，要判别其为错误的分布 $(1-y_i)$

对于单个样本对 $(x_1,y_1)$ 来说，$y_1$ 为真实样本分布，那么对应的 $1-y_1$ 就是生成样本分布，则 $D(x_1)$ 可表示为判别样本为正确的概率，$1-D(x_1)$ 为判别样本为错误的概率，故有：

$$\mathbb{H}((x_1,y_1),D) = -y_1\log D(x_1) -(1-y_1)\log (1-D(x_1))$$

将其推广到 $n$ 个样本上，有：

$$\mathbb{H}((x_1,y_1)^n_{i=1},D) = -\sum_{i=1}^n y_i\log D(x_i) -\sum_{i=1}^n (1-y_i)\log (1-D(x_i))$$

为便于表达，令 $y_i=\frac{1}{2}$，$G(z)$ 表示生成样本，将上式写为概率分布的期望形式，有：

$$\mathbb{H}((x_1,y_1)^{\infty}_{i=1},D) = -\frac{1}{2}\mathbb{E}_{x\sim p_{\text{data}}} \Big[ \log D(x) \Big] -\frac{1}{2} \mathbb{E}_{z\sim p_z(z)} \Big[ \log (1-D(G(z))) \Big]$$

用 $V(G,D)$ 来表示真实样本和生成样本的差异程度，那么损失函数的优化目标可写为：

$$\min_{G} \max_{D} V(D,G) = \mathbb{E}_{x\sim p_{\text{data}}} \Big[ \log D(x) \Big] + \mathbb{E}_{z\sim p_z(z)} \Big[ \log (1-D(G(z))) \Big]$$

对于生成器 G，其目标是让判别器 D 认为生成的数据是真的（概率 $1$），而对于判别器 $D$，其目标是让真实数据为真（概率 $1$），生成数据为假（概率 $0$）

也就是说，优化目标可以理解为：

• $\max\limits_D V(D,G)$：固定生成器 G，尽可能地让判别器 D 能够最大化地判别出样本来自于真实数据还是生成数据
• 令 $L=\max\limits_{D} V(D,G)$，有 $\min\limits_G L$：固定判别器 D，最小化真实样本与生成样本的差异

【不足】

GAN 的巧妙在于其设计思维，而技术上是对现有算法的组合，其不可避免的存在一些不足

1. 需要同时训练生成器 G 和判别器 D 两个网络，训练难度大
2. 训练过程中可能会发生崩溃问题，使得生成器 G 退化，总是生成同样的样本点，无法继续学习，同时，当生成器 G 崩溃时，判别器 D 也会对相似的样本点指向相似的方向，使得训练无法继续
3. 网络难以收敛，目前所有理论都认为 GAN 应该在纳什均衡上有很好的表现，但梯度下降只有在凸函数的情况下才能保证实现纳什均衡
4. 可解释性差，生成器的分布 $p_z(z)$​ 没有显式表达
5. 多样性差，生成器的关注点在于只需要骗过判别器
6. 难以学习生成离散数据