变分自编码器 VAE

【概述】

变分自编码器（Variational Auto-Encoders，VAE）是深度生成模型的一种形式，是由 Kingma 等人于 2014 年提出的基于变分贝叶斯（Variational Bayes，VB）推断的生成式网络结构

与传统的自编码器 AE 通过数值的方式描述潜在空间不同，它以概率的方式描述对潜在空间的观察，在数据生成方面表现出了巨大的应用价值

VAE 一经提出就迅速获得了深度生成模型领域广泛的关注，并和生成对抗网络 GAN 被视为无监督式学习领域最具研究价值的方法之一，在深度生成模型领域得到越来越多的应用

【从 AE 到 VAE】

VAE 继承了传统 AE 的架构，并用其来学习数据生成分布，具体来说，其与自编码器的不同点在于：AE 的编码器是学习输入 $X$ 的潜在表示 $\mathbf{h}$ ，中间输出的是 $\mathbf{h}$ 的具体取值，VAE 的编码器是学习输入 $X$ 的潜在空间 $Z$，中间输出的是 $Z$ 的具体分布，这样一来，就可以从这个分布中进行采样，然后送入到解码器，由解码器还原并生成类似输入样本 $X$ 的样本 $\hat{X}$

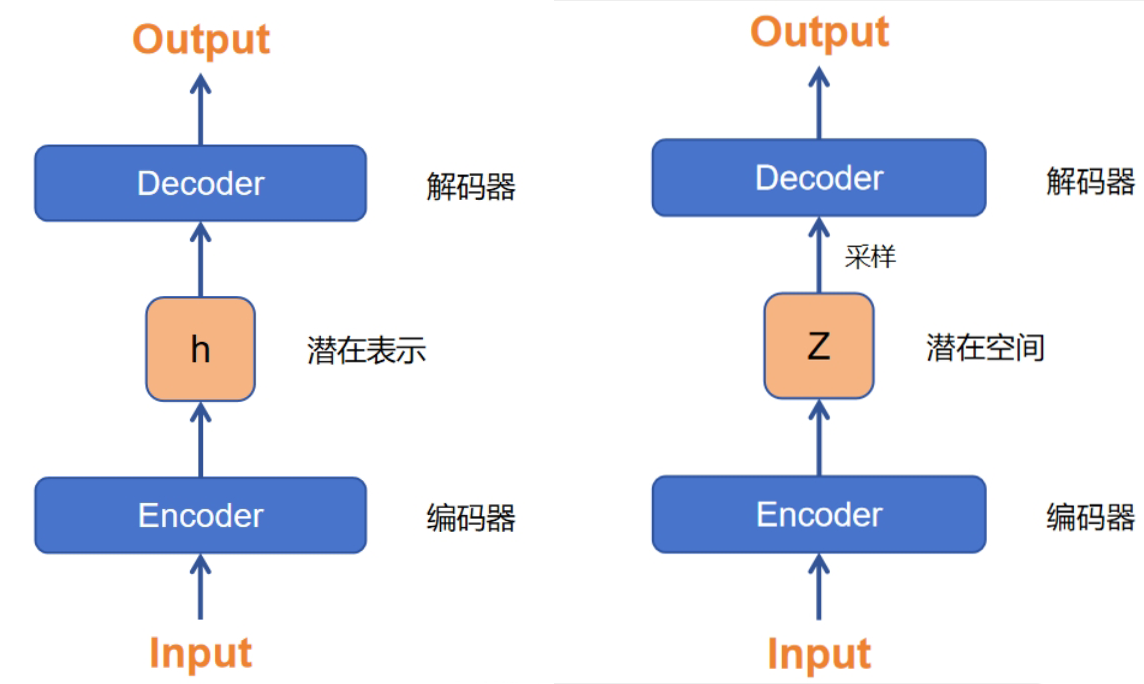
VAE 采用变分推断的方法，整个编码器和解码器就是变分推断的过程，对于最大化 $\mathbb{E}_{z\sim q(z|x)}[\log p(x|z)]$ 的过程，就是模型想要尽可能地从潜在空间 $Z$ 中重组 $x$，也就是从解码器 Decoder 上下手；而对于最小化 $D_{KL}[q(z|x) || \log p(z)]$ 的过程，就是模型想要尽可能地让 $z$ 避免过拟合，使得 $z$ 的近似后验分布 $q(z|x)$ 尽可能接近其先验分布 $p(z)$，即也就是从编码器 Encoder 上下手

【模型架构】

基本架构

对于最小化 $D_{KL}[q(z|x) || \log p(z)]$ 来说，核心问题就是要确定潜在空间 $Z$，VAE 认为 $Z$ 没有一种合适的阐述方式，只是直接假定 $Z$ 的样本可以从采用标准正态分布 $\mathcal{N}(\mathbf{0},\mathbf{I})$ 中抽取，因为任意维度 $d$ 的分布都可以用一组 $d$ 个服从高斯分布的变量，通过复杂函数映射而生成

那么此时问题就转化为找到一个合适的映射函数并获取其输出，即高斯分布的均值和方差，VAE 采用两个神经网络分别输出均值和方差，即：

$$\begin{gather*} \mu = f_1(X) \\ \log \sigma^2 = f_2(X) \end{gather*}$$

其中，$f_1(\cdot)$ 和 $f_2(\cdot)$ 分别代表两个独立的神经网络，拟合 $\log \sigma^2$ 是因为 $\sigma^2$ 本身非负，需要加激活函数，而直接拟合 $\log \sigma^2$ 就不需要再加额外的激活函数了

此时，近似后验分布 $q(z|x)$ 就可以描述为：

$$q(z|x) = \mathcal{N}(z;\mu,\sigma^2\mathbf{I})$$

这样一来，整个模型的架构就十分清晰了：

1. 样本进入编码器 Encoder，学习并输出潜在空间的均值和方差，得到潜在空间 $Z$
2. 从潜在空间 $Z$ 中采样，并进入解码器 Decoder，Decoder 根据采样进行重构，重新生成样本

根据目标函数，要保证重构尽可能的准确，同时令潜在空间接近标准正态分布，即最大化变分下界 ELBO，可以直接对变分下界 ELBO 取反作为损失函数，即：

$$\mathcal{L} = - \mathbb{E}_{z\sim q(z|x)}[\log p(x|z)] + D_{KL}[q(z|x) \parallel \log p(z)]$$

根据上面的理论，可以画出模型架构图：

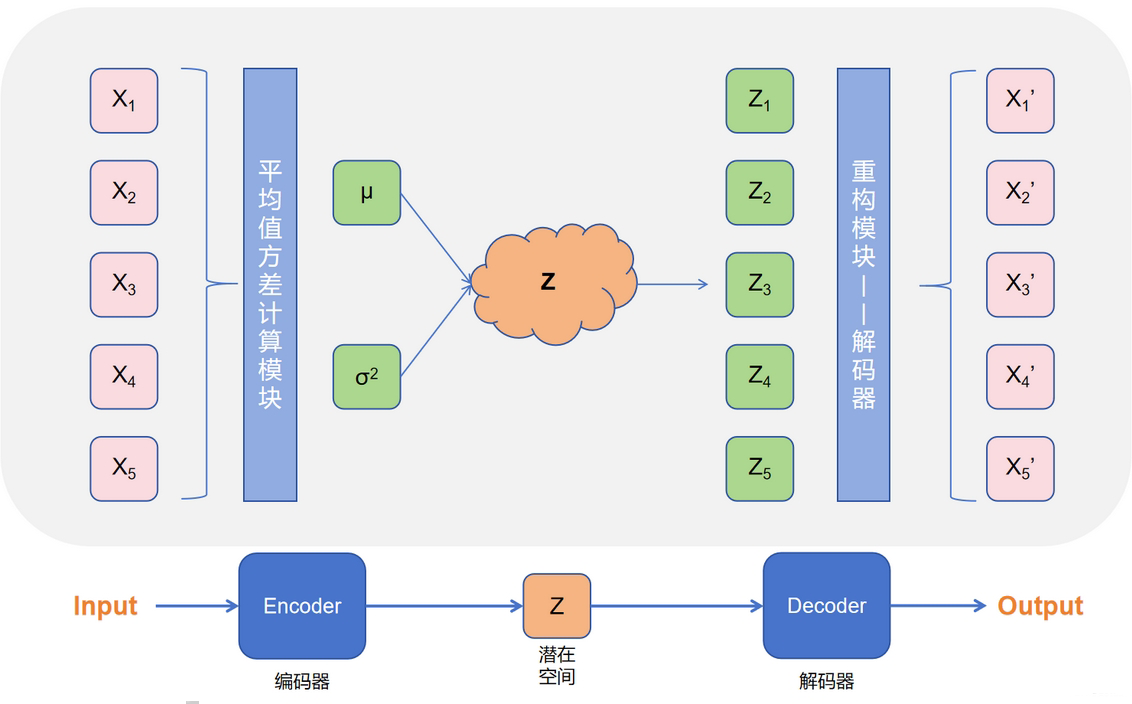
架构调整

根据损失函数 $\mathcal{L}$，需要对比原始样本 $X$ 和生成样本 $X’$，但问题在于如何对比？

• 使用 KL 散度： KL 散度是根据两个概率分布的表达式来算相似度的，但只有一批从真实的分布采样而来的数据（训练集）$\{X_1, X_2,\cdots,X_n\}$，和一批从构造的分布 $Z$ 采样重构而来的数据（生成集） $\{X_1’,X_2’,\cdots,X_n’\}$，只知道样本本身，没有分布表达式
• 直接计算距离：并不知道训练集和生成集的对应关系，即 $X_1$ 不一定对应着 $X_1’$

基于这个问题，VAE 采用了一种迂回方式，既然无法找到对应关系，那就一对一的进行训练，每个真实样本都计算其独有的均值和方差，构造其专有的潜在空间，这样就有了每一个样本 $X_k$ 对应的潜在空间 $Z$，以及采样并重构后的生成样本 $X_k’$

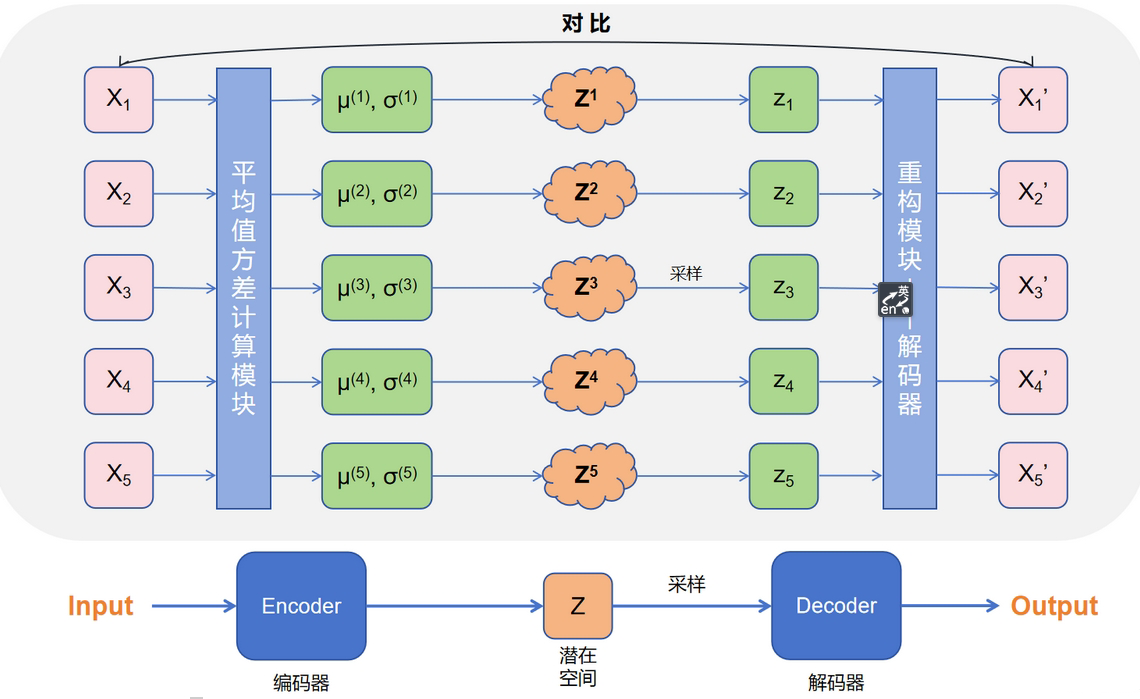
此时损失函数就变为：

$$\mathcal{L}(\theta,\phi;x_i) = - \mathbb{E}_{z\sim q_{\phi}(z|x_i)}[\log p_{\theta}(x_i|z)] + D_{KL}[q_{\phi}(z|x_i) \parallel \log p(z)]$$

其中，$\phi$ 是编码器 Encoder 的参数，$\theta$ 是解码器 Decoder 的参数

同时，对近似后验分布重新描述：

$$q(z|x_i) = \mathcal{N}(z;\mu_i,\sigma^2_i\mathbf{I})$$

损失函数的理解

当有了模型架构后，重新来看损失函数

$$\mathcal{L}(\theta,\phi;x_i) = - \mathbb{E}_{z\sim q_{\phi}(z|x_i)}[\log p_{\theta}(x_i|z)] + D_{KL}[q_{\phi}(z|x_i) \parallel \log p(z)]$$

第一项很自然的，就是重构项和对应的样本之间的差距，越小越好，然而在整个模型中的重构样本 $Z_k$ 是通过采样得到的，并不是像常规 AE 那样由 Encoder 直接计算得到，因此这部分也就相当于噪声，它的随机性在干扰重构的过程，因此在训练过程中，为了更好重构，模型会尽可能让潜在空间的方差变为 $0$，进而退化成普通的 AE，这样一来，所谓的生成式模型就名存实亡了

此时，损失函数的第二项就起到了作用，它让潜在空间的后验分布逼近标准正态分布 $\mathcal{N}(\mathbf{0}, \mathbf{I})$，从而避免了随机性消失（方差变成 $0$），相当于对训练过程的正则化

因此，常称损失函数中的第一项 $- \mathbb{E}_{z\sim q_{\phi}(z|x_i)}[\log p_{\theta}(x_i|z)] $ 为重构项（Reconstruction Term），第二项 $D_{KL}[q_{\phi}(z|x_i) || \log p(z)]$ 为正则化项（Regularization Term）

传统的 AE 编码器 Encoder 生成的是有关样本的潜在表示，是一个确定的值，而 VAE 的编码器 Encoder 生成的是一个潜在空间，更具体的说是生成专属于当前样本的平均值和方差，这样算出来的值是不确定的，而从这样的潜在空间采样后再进行重构，这一过程就相当于给潜在表示添加噪声，相当于对编码器 Encoder 的正则化，使得解码器 Decoder 能够对噪声具有一定的鲁棒性

而对另一个计算方差的网络来说，其就可以理解为一个对噪声大小的调节器：方差越大，采样结果就越分散，变相增加了重构的难度；方差越小，采样结果就越集中，变相降低了重构的难度

说白了，重构的过程是希望没有噪声的，而 KL 损失则希望有高斯噪声的，两者是对立的，所以，VAE 与 GAN 其实十分相似，内部都包含了生成和对抗的过程，只不过在 VAE 中，生成和对抗这两者是混合起来共同进化的

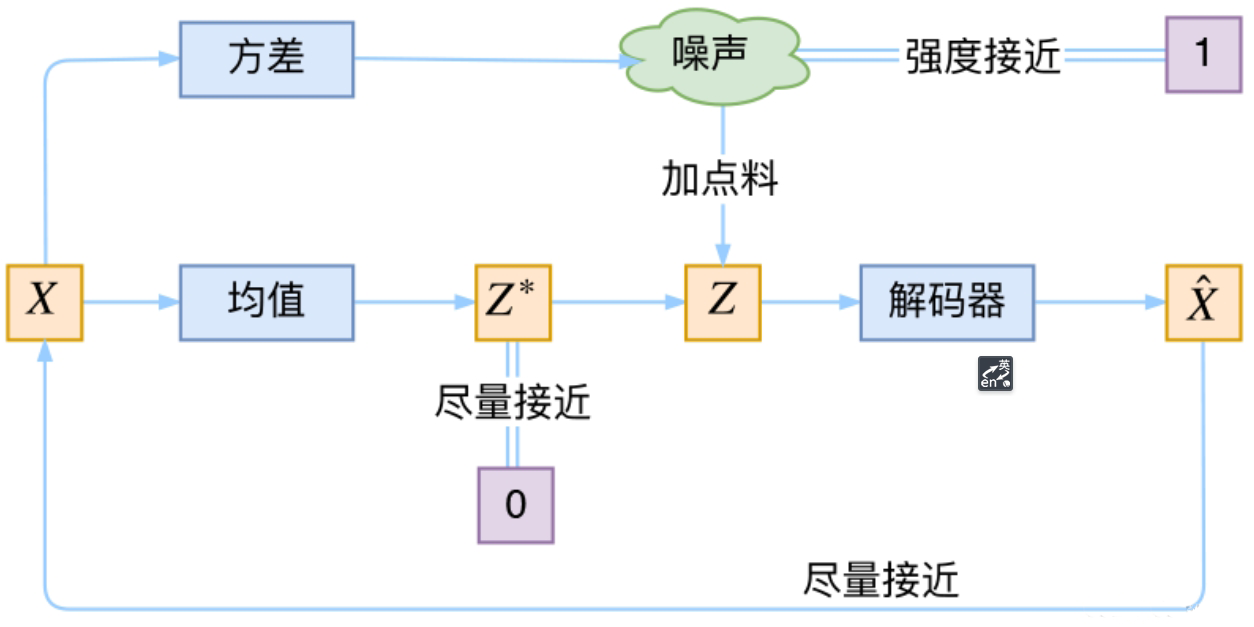
重参数技巧

在整个过程中，从潜在空间 $Z$ 中采样才得到潜在表示 $Z_k$ 的，而恰恰采样这个操作是不可导的，这也就导致在训练过程中无法进行反向传播，就无法进行训练了，为了解决这个问题，VAE 使用了重参数技巧（Reparameterization Trick）

对于潜在空间 $Z$，利用正态分布标准化，有：

$$Z\sim \mathcal{N}(\mu,\sigma^2) \rightarrow \frac{Z-\mu}{\sigma} \sim \mathcal{N}(\mathbf{0},\mathbf{I})$$

即 $\frac{Z-\mu}{\sigma}$ 服从于均值为 $0$，方差为 $1$ 的标准正态分布 $\mathcal{N}(\mathbf{0},\mathbf{I})$

由此，引入噪声项：

$$\varepsilon = \frac{z-\mu}{\sigma}$$

这样一来，将原本从 $\mathcal{N}(\mu,\sigma^2)$ 采样得到 $z$ 的操作，转换成了从 $\mathcal{N}(\mathbf{0},\mathbf{I})$ 中采样一个 $\varepsilon$，再令：

$$z=\mu + \varepsilon \sigma$$

使得梯度计算可以通过 $\mu$ 和 $\sigma$ 直接传递，而不再涉及对随机采样的梯度